
【題目】如圖1所示,![]() 為矩形
為矩形![]() 的邊
的邊![]() 上一點(diǎn),動(dòng)點(diǎn)
上一點(diǎn),動(dòng)點(diǎn)![]() 同時(shí)從點(diǎn)
同時(shí)從點(diǎn)![]() 出發(fā),點(diǎn)
出發(fā),點(diǎn)![]() 沿折線
沿折線![]() 運(yùn)動(dòng)到點(diǎn)
運(yùn)動(dòng)到點(diǎn)![]() 時(shí)停止,點(diǎn)
時(shí)停止,點(diǎn)![]() 沿
沿![]() 運(yùn)動(dòng)到點(diǎn)
運(yùn)動(dòng)到點(diǎn)![]() 時(shí)停止,它們運(yùn)動(dòng)的速度都是
時(shí)停止,它們運(yùn)動(dòng)的速度都是![]() 秒.設(shè)
秒.設(shè)![]() 同時(shí)出發(fā)
同時(shí)出發(fā)![]() 秒時(shí),
秒時(shí),![]() 的面積為
的面積為![]() ,已知
,已知![]() 與
與![]() 的函數(shù)關(guān)系圖象如圖2所示.請(qǐng)回答:
的函數(shù)關(guān)系圖象如圖2所示.請(qǐng)回答:
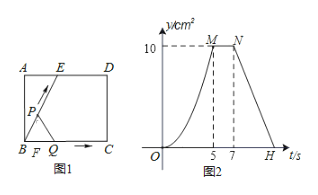
(1)線段![]() 的長(zhǎng)為_______cm;
的長(zhǎng)為_______cm;
(2)當(dāng)運(yùn)動(dòng)時(shí)間![]() 秒時(shí),
秒時(shí),![]() 之間的距離是_______
之間的距離是_______![]() .
.
【答案】5 ![]()
【解析】
(1)根據(jù)圖2可以判斷三角形的面積變化分為三段,可以判斷出當(dāng)點(diǎn)P到達(dá)點(diǎn)E時(shí)點(diǎn)Q到達(dá)點(diǎn)C,從而得到BC的長(zhǎng)度;
(2)如圖1,過(guò)點(diǎn)P作PF⊥BC于點(diǎn)F,根據(jù)面積不變時(shí)△BPQ的面積為10,可得AB=4,由矩形的性質(zhì)和銳角三角函數(shù)的定義求得PF的長(zhǎng)度,然后在直角△PBF中,由勾股定理求得BF=1.5,再在直角△PFQ中,由勾股定理求得PQ的長(zhǎng)度.
解:(1)根據(jù)圖2可得,當(dāng)點(diǎn)P到達(dá)點(diǎn)E時(shí),點(diǎn)Q到達(dá)點(diǎn)C,
∵點(diǎn)P、Q的運(yùn)動(dòng)的速度都是1cm/s,
∴BC=BE=5cm,
故答案是:5;
(2)如圖1,過(guò)點(diǎn)P作PF⊥BC于點(diǎn)F,
根據(jù)面積不變時(shí)△BPQ的面積為10,可得AB=4,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB=![]() ,
,
∴PF=PBsin∠PBF=2.5×![]()
∴在直角△PBF中,由勾股定理得到:BF=![]() ,
,
∴FQ=2.5-1.5=1,
∴在直角△PFQ中,由勾股定理得到:PQ=![]() ,
,
故答案是:![]() .
.




| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】近年來(lái)佳木斯市旅游事業(yè)發(fā)展迅速,“大亮子河森林公園”“富錦國(guó)家濕地公園”“赫哲民族文化村”“大來(lái)崗達(dá)勒花海”等景區(qū)愈來(lái)愈為人們所知曉 . 在一次調(diào)查中,根據(jù)市民對(duì)這四個(gè)景區(qū)的了解情況,按答題分?jǐn)?shù)分為![]() . 比較熟悉;
. 比較熟悉; ![]() . 基本了解;
. 基本了解; ![]() . 略有知曉;
. 略有知曉; ![]() . 知之甚少,四類進(jìn)行統(tǒng)計(jì),繪制了以下兩幅統(tǒng)計(jì)圖(不完整),請(qǐng)根據(jù)圖中信息解答以下各題:
. 知之甚少,四類進(jìn)行統(tǒng)計(jì),繪制了以下兩幅統(tǒng)計(jì)圖(不完整),請(qǐng)根據(jù)圖中信息解答以下各題:
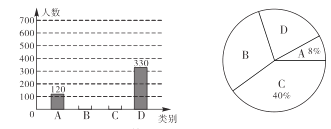
(1)本次調(diào)查活動(dòng)的樣本容量是 ;
(2)補(bǔ)全條形統(tǒng)計(jì)圖;
(3)“略有知曉”類占扇形統(tǒng)計(jì)圖的圓心角是多少度? “知之甚少”類市民占被調(diào)查人數(shù)的百分比是多少?
(4)已知某小區(qū)有 5000 人,那么估計(jì)對(duì)這些景區(qū)“比較熟悉”的有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖1,在![]() 中,弦
中,弦![]() 弦
弦![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() ,連接
,連接![]() 、
、![]() 、
、![]() ,
,![]() .
.
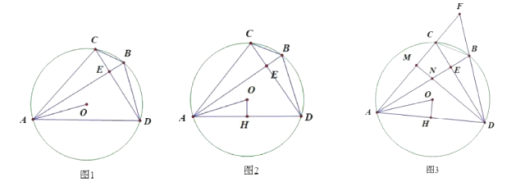
(1)求證:![]()
(2)如圖2,過(guò)點(diǎn)![]() 作
作![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() ,求證:
,求證:![]()
(3)如圖3,在(2)的條件下,延長(zhǎng)![]() 、
、![]() 交于點(diǎn)
交于點(diǎn)![]() ,過(guò)點(diǎn)
,過(guò)點(diǎn)![]() 作
作![]() ,垂足為
,垂足為![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的長(zhǎng).
的長(zhǎng).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】轉(zhuǎn)轉(zhuǎn)盤(pán)和摸球是等可能概率下的經(jīng)典模型.
(1)在一個(gè)不透明的口袋中,放入除顏色外其余都相同的4個(gè)小球,其中1個(gè)白球,3個(gè)黑球攪勻后,隨機(jī)同時(shí)摸出2個(gè)球,求摸出兩個(gè)都是黑球的概率(要求釆用樹(shù)狀圖或列表法求解);
(2)如圖,轉(zhuǎn)盤(pán)的白色扇形和黑色扇形的圓心角分別為120°和240°.讓轉(zhuǎn)盤(pán)自由轉(zhuǎn)動(dòng)2次,求指針2次都落在黑色區(qū)域的概率(要求采用樹(shù)狀圖或列表法求解).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,CD是⊙O的弦,AB是直徑,且CD∥AB,連接AC、AD、OD,其中AC=CD,過(guò)點(diǎn)B的切線交CD的延長(zhǎng)線于E.
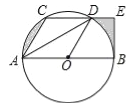
(1)求證:DA平分∠CDO;
(2)若AB=12,求圖中陰影部分的周長(zhǎng)之和(參考數(shù)據(jù):π=3.1,![]() =1.4,
=1.4,![]() =1.7).
=1.7).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
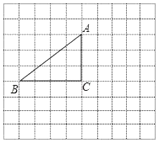
【題目】如圖,將△ABC放在每個(gè)小正方形的邊長(zhǎng)為1的網(wǎng)格中,點(diǎn)A、點(diǎn)B、點(diǎn)C均落在格點(diǎn)上
(Ⅰ)線段AB的長(zhǎng)度=________;
(Ⅱ)請(qǐng)?jiān)谌鐖D所示的網(wǎng)格中,用無(wú)刻度的直尺,在∠ABC的平分線上找一點(diǎn)P,在BC上找一點(diǎn)Q,使CP+PQ的值最小,并簡(jiǎn)要說(shuō)明點(diǎn)P,Q的位置是如何找到的_____________(不要求證明).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:拋物線l,y=x2+bx+c與x軸交于點(diǎn)A和點(diǎn)B(3,0),與y軸交于點(diǎn)C(0,﹣3).
(1)求拋物線l的頂點(diǎn)P的坐標(biāo)為的A的坐標(biāo);
(2)將拋物線l先向上平移3個(gè)單位長(zhǎng)度,再向左平移2個(gè)單位長(zhǎng)度,得到拋物線l1,請(qǐng)直接寫(xiě)出平移后的拋物線l1的表達(dá)式;
(3)將拋物線l向右平移m個(gè)單位長(zhǎng)度,得到拋物線l2,其中點(diǎn)A的對(duì)應(yīng)點(diǎn)為點(diǎn)M,若點(diǎn)M、A、P是恰好一個(gè)矩形的三個(gè)頂點(diǎn),請(qǐng)求出m的值
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
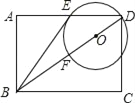
【題目】已知:如圖,在矩形ABCD中,點(diǎn)O在對(duì)角線BD上,以OD的長(zhǎng)為半徑的⊙O與AD,BD分別交于點(diǎn)E、點(diǎn)F,且∠ABE=∠DBC.
(1)判斷直線BE與⊙O的位置關(guān)系,并證明你的結(jié)論;
(2)若sin∠ABE=![]() ,CD=2,求⊙O的半徑.
,CD=2,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】小昕的口袋中有5把相似的鑰匙,其中2把鑰匙(記為A1,A2)能打開(kāi)教室前門(mén)鎖,而剩余的3把鑰匙(記為B1,B2,B3)不能打開(kāi)教室前門(mén)鎖.
(1)小昕從口袋中隨便摸出一把鑰匙就能打開(kāi)教室前門(mén)鎖的概率是 ;
(2)請(qǐng)用樹(shù)狀圖或列表等方法,求出小昕從口袋中第一次隨機(jī)摸出的一把鑰匙不能打開(kāi)教室前門(mén)鎖(摸出的鑰匙不再放回),而第二次隨機(jī)摸出的一把鑰匙正好能打開(kāi)教室前門(mén)鎖的概率.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com