
【題目】如圖,直線AB與CD相交于點O, ![]() .
.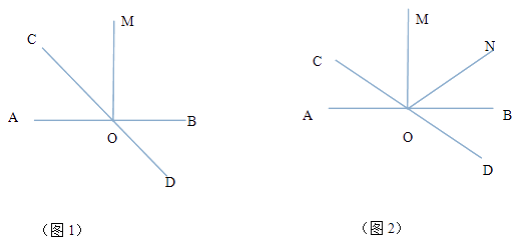
(1)如圖1,若OC平分 ![]() ,求
,求 ![]() 的度數;
的度數;
(2)如圖2,若 ![]() ,且OM平分
,且OM平分 ![]() ,求
,求 ![]() 的度數.
的度數.
【答案】
(1)解:∵∠AOM=90°,OC平分∠AOM
∴∠AOC= ![]() ∠AOM=45°
∠AOM=45°
∵∠AOC+∠AOD=180°
∴∠AOD=180°-∠AOC=180°-45°=135°
(2)解:∵∠BOC=4∠NOB
∴設∠NOB=x°,∠BOC=4x°
∴∠CON=∠COB-∠BON=4x°-x°=3x°
∵OM平分∠CON
∴∠COM=∠MON= ![]() ∠CON=
∠CON= ![]() x°
x°
∵ ![]()
解得:x=36
∴∠MON= ![]() x°=
x°= ![]() ×36°=54°
×36°=54°
即∠MON的度數為54°
【解析】(1)根據OC平分 ∠AOM求出∠AOC的度數,再根據鄰補角的定義求出∠AOD的度數即可。
(2)設∠NOB=x°,利用∠BOC=4∠NOB,表示出∠BOC的度數,從而得出∠CON的度數,再根據角平分線的定義得出∠COM=∠MON,再根據∠NOB+∠MON=90°,建立方程求解,再求出∠MON的度數。


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:
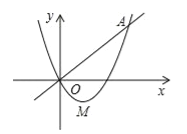
【題目】如圖,在平面直角坐標系xOy中,一次函數y=x與二次函數![]() 的圖象相交于O、A兩點,點A(3,3),點M為拋物線的頂點.
的圖象相交于O、A兩點,點A(3,3),點M為拋物線的頂點.
(1)求二次函數的表達式;
(2)長度為![]() 的線段PQ在線段OA(不包括端點)上滑動,分別過點P、Q作x軸的垂線交拋物線于點P1、Q1,求四邊形PQQ1P1面積的最大值;
的線段PQ在線段OA(不包括端點)上滑動,分別過點P、Q作x軸的垂線交拋物線于點P1、Q1,求四邊形PQQ1P1面積的最大值;
(3)直線OA上是否存在點E,使得點E關于直線MA的對稱點F滿足S△AOF=S△AOM?若存在,求出點E的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】重慶一中渝北分校積極組織學生開展課外閱讀活動,為了解全校學生每周課外閱讀的時間量t(單位:小時),采用隨機抽樣的方法抽取部分學生進行了問卷調查,調查結果按0≤t<2,2≤t<3,3≤t<4,t≥4分為四個等級,并分別用A、B、C、D表示,根據調查結果統計數據繪制成了如圖所示的兩幅不完整的統計圖,由圖中給出的信息解答下列問題: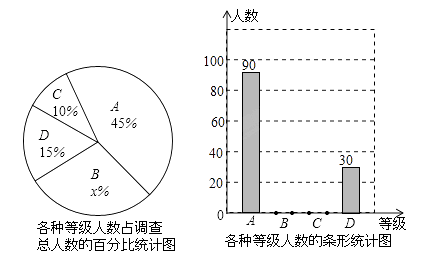
(1)求這次抽查的學生總數是多少人,并求出x的值;
(2)將不完整的條形統計圖補充完整;
(3)若該校共有學生3600人,試估計每周課外閱讀時間量滿足2≤t<4的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解方程組的基本思想是_________,也就是把二元一次方程組轉化為______________. 消元的方法有:_____________、_______________等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲、乙兩動點分別從正方形ABCD的頂點A、C同時沿正方形的邊開始移動,甲點依順時針方向環行,乙點依逆時針方向環行.若甲的速度是乙的速度的3倍,則它們第2015次相遇在邊 上.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com