
| 3 |
| 1 |
| 2 |

| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
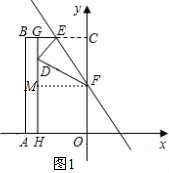
| EG |
| ED |
| 1 |
| 2 |
| 120 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| ||
| 2 |
| 3 |
| ||
| 2 |
3
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
3
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|
|
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
| 3 |
| 3 |
3
| ||
| 2 |
| 9 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
5
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 2 |
3
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 3 |
3
| ||
| 2 |
| 3 |
| 3 |
| 3 |
| 9 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
| 3 |
| 2 |
5
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:
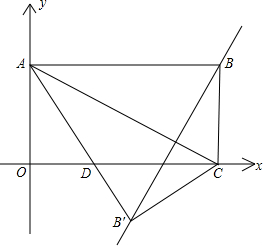 如圖,矩形OABC在平面直角坐標系中,若OA、OC的長滿足|OA-2|+(OC-2
如圖,矩形OABC在平面直角坐標系中,若OA、OC的長滿足|OA-2|+(OC-2| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
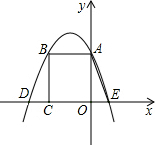 如圖,矩形OABC在平面直角坐標系中的位置如圖所示,OA=3,AB=2.拋物線y=ax2+bx+c(a≠0)經過點A和點B,與x軸分別交于點D、E(點D在點E左側),且OE=1,則下列結論:
如圖,矩形OABC在平面直角坐標系中的位置如圖所示,OA=3,AB=2.拋物線y=ax2+bx+c(a≠0)經過點A和點B,與x軸分別交于點D、E(點D在點E左側),且OE=1,則下列結論:查看答案和解析>>
科目:初中數學 來源: 題型:
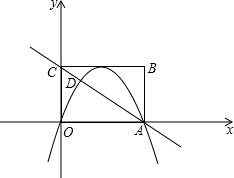 (2013•昆明)如圖,矩形OABC在平面直角坐標系xOy中,點A在x軸的正半軸上,點C在y軸的正半軸上,OA=4,OC=3,若拋物線的頂點在BC邊上,且拋物線經過O,A兩點,直線AC交拋物線于點D.
(2013•昆明)如圖,矩形OABC在平面直角坐標系xOy中,點A在x軸的正半軸上,點C在y軸的正半軸上,OA=4,OC=3,若拋物線的頂點在BC邊上,且拋物線經過O,A兩點,直線AC交拋物線于點D.查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•浙江二模)如圖,矩形OABC在平面直角坐標系中,A(0,3),C(4,0),點P為直線AB上一動點,將直線OP繞點P逆時針方向旋轉90°交直線BC于點Q,當△POQ為等腰三角形時,點P坐標為
(2012•浙江二模)如圖,矩形OABC在平面直角坐標系中,A(0,3),C(4,0),點P為直線AB上一動點,將直線OP繞點P逆時針方向旋轉90°交直線BC于點Q,當△POQ為等腰三角形時,點P坐標為查看答案和解析>>
科目:初中數學 來源: 題型:
 按順時針方向旋轉135°,得到矩形EFGH(點E與O重合).
按順時針方向旋轉135°,得到矩形EFGH(點E與O重合).| 2 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com