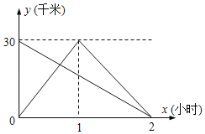
【題目】在一條筆直的公路上有AB兩地，小明騎自行車從A地去B地，小剛騎電動車從B地去A地然后立即原路返回到B地，如圖是兩人離B地的距離y(千米)和行駛時間x(小時)之間的函數圖象．請根據圖象回答下列問題：
(1)AB兩地的距離是_____，小明行駛的速度是_____.
(2)若兩人間的距離不超過3千米時，能夠用無線對講機保持聯系，那么小剛從A地原路返回到B地途中，兩人能夠用無線對講機保持聯系的x的取值范圍是______．
【答案】(1)30km；15km/h；(2)
.
【解析】
(1)根據圖象即可解決問題；
(2)根據圖象和待定系數法分別求出小剛從A地原路返回到B地時對應的一次函數
和小明從A地到B地對應的一次函數
，再求出當
時x的值即可求出答案．
解：(1)x＝0時，小明距離B地30km，所以，A、B兩地的距離為30km；
由圖可知，小明行駛的速度：30÷2＝15(km/h)，小剛行駛的速度：30÷1＝30(km/h)，
(2)設小剛從A地原路返回到B地時對應的一次函數解析式為
，小明從A地到B地對應的一次函數解析式為
，則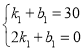
，
，
解得：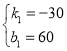
，
，
∴
，
，
根據題意，當時，
，解得
，
所以，當時，小剛從A地原路返回到B地途中，兩人能夠用無線對講機保持聯系．
故答案為：(1)30km；15km/h；(2)．
智趣寒假作業云南科技出版社系列答案科目：初中數學 來源： 題型：
【題目】如圖，半圓O的直徑AB＝10，有一條定長為6的動弦CD在弧AB上滑動（點C、點D分別不與點A、點B重合），點E、F在AB上，EC⊥CD，FD⊥CD．
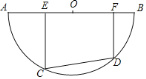
（1）求證：EO＝OF；
（2）聯結OC，如果△ECO中有一個內角等于45°，求線段EF的長；
（3）當動弦CD在弧AB上滑動時，設變量CE＝x，四邊形CDFE面積為S，周長為l，問：S與l是否分別隨著x的變化而變化？試用所學的函數知識直接寫出它們的函數解析式及函數定義域，以說明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，四邊形ABCD中，DB⊥BC，DB平分∠ADC，點E為邊CD的中點，AB⊥BE．
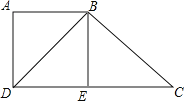
（1）求證：BD2＝ADDC；
（2）連結AE，當BD＝BC時，求證：ABCE為平行四邊形．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知梯形ABCD中，AD∥BC，AC、BD相交于點O，AB⊥AC，AD＝CD，AB＝3，BC＝5．求：
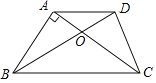
（1）tan∠ACD的值；
（2）梯形ABCD的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，某大樓的頂部豎有一塊廣告牌CD，小李在山坡的坡腳A處測得廣告牌底部D的仰角為60°沿坡面AB向上走到B處測得廣告牌頂部C的仰角為45°，已知山坡AB的傾斜角∠BAH＝30°，AB＝20米，AB＝30米．
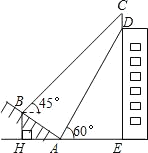
（1）求點B距水平面AE的高度BH；
（2）求廣告牌CD的高度．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，E、F分別為正方形ABCD的邊AB、AD上的點，且AE=AF，聯接EF，將△AEF繞點A逆時針旋轉45°，使E落在E
，F落在F，聯接BE并延長交DF于點G，如果AB=
，AE=1，則DG=______.
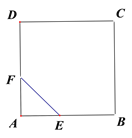
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某林業部門統計某種樹苗在本地區一定條件下的移植成活率，結果如表：
移植的棵數 | 300 | 700 | 1000 | 5000 | 15000 |
成活的棵數 | 280 | 622 | 912 | 4475 | 13545 |
成活的頻率 | 0.933 | 0.889 | 0.912 | 0.895 | 0.903 |
根據表中的數據，估計這種樹苗移植成活的概率為_____（精確到0.1）；如果該地區計劃成活4.5萬棵幼樹，那么需要移植這種幼樹大約_____萬棵．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】假期小穎決定到游泳館游泳，游泳館門票有兩種：
種是每天購票進館，沒有優惠；
種是每月先購買貴賓卡，持貴賓卡購票每張可減少8元．設小穎游泳
次，
（元）是按種購票方案的費用，
（元）是按種購票方案的費用根據圖中信息解答問題：
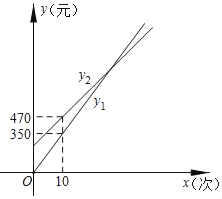
（1）按種方案購票，每張門票價格為 元；
（2）按種方案購票，求與的函數解析式；
（3）如果小穎假期30天，每天都到游泳館游泳一次，通過計算她選擇哪種購票方案比較合算．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
