
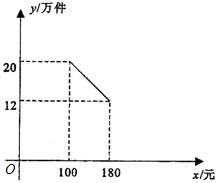
 該產品銷售量y(萬件)與產品售價x(元)之間的函數關系如圖所示.
該產品銷售量y(萬件)與產品售價x(元)之間的函數關系如圖所示. ,
, ,b=30,
,b=30, x+30,100≤x≤180;
x+30,100≤x≤180; x2+36x-3300=-
x2+36x-3300=- (x-180)2-60≤-60,
(x-180)2-60≤-60, x2+36x-1800,
x2+36x-1800, x2+36x-1800-60=1340,
x2+36x-1800-60=1340, (x-180)2-60≤-60,則第一年公司虧損了,當產品售價定為180元/件時,虧損最小,最小虧損為60萬元;
(x-180)2-60≤-60,則第一年公司虧損了,當產品售價定為180元/件時,虧損最小,最小虧損為60萬元; x2+36x-1800-60=1340,解得x的值,根據100≤x≤180,則x=160時,公司兩年共盈利達1340萬元.
x2+36x-1800-60=1340,解得x的值,根據100≤x≤180,則x=160時,公司兩年共盈利達1340萬元.

科目:初中數學 來源: 題型:
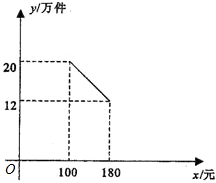 該產品銷售量y(萬件)與產品售價x(元)之間的函數關系如圖所示.
該產品銷售量y(萬件)與產品售價x(元)之間的函數關系如圖所示.查看答案和解析>>
科目:初中數學 來源:2011年湖北省鄂州市宅俊中學中考數學模擬試卷(二)(解析版) 題型:解答題

查看答案和解析>>
科目:初中數學 來源:2011年湖北省武漢市四月調考九年級數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com