
 的交點
的交點 的圖象上另取一點B,作BK⊥x軸于K,將(2)中的一次函數圖象繞點A旋轉后所得的直線記為l,若l與y軸的正半軸交于點C,且4CO=FO.試問:在y軸上是否存在點P,使得兩個三角形的面積S△PCA=S△BOK?若存在,求點P的坐標,若不存在,請說明理由.
的圖象上另取一點B,作BK⊥x軸于K,將(2)中的一次函數圖象繞點A旋轉后所得的直線記為l,若l與y軸的正半軸交于點C,且4CO=FO.試問:在y軸上是否存在點P,使得兩個三角形的面積S△PCA=S△BOK?若存在,求點P的坐標,若不存在,請說明理由.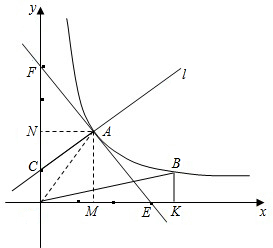
 中,得
中,得
 ,2),
,2),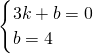 .解得
.解得

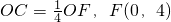
 上,則有xB•yB=3,
上,則有xB•yB=3,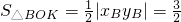
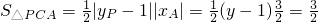
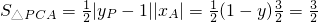
 .再根據點A的橫坐標,知PC的長應是2.根據題意可以首先求得點C的坐標,再根據點P可能在點C的上方或下方進行分析.
.再根據點A的橫坐標,知PC的長應是2.根據題意可以首先求得點C的坐標,再根據點P可能在點C的上方或下方進行分析.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
| 3 |
 =2,∠ADC=30°
=2,∠ADC=30°查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com