
【題目】已知,在![]() 中,
中,![]() ,點
,點![]() 為直線
為直線![]() 上一動點(點
上一動點(點![]() 不與點
不與點![]() 重合).以
重合).以![]() 為邊作正方形
為邊作正方形![]() 連接
連接![]() .
.
觀察猜想:
(1)如圖1,當點![]() 在線段
在線段![]() 上時,判斷
上時,判斷![]() 之間數量關系,并證明;
之間數量關系,并證明;



類比探究:
(2)如圖2,當點![]() 在線段
在線段![]() 的延長線上時,其他條件不變,請直接寫出
的延長線上時,其他條件不變,請直接寫出![]() 三條線段之間的關系;
三條線段之間的關系;
拓展延伸:
(3)如圖3,當點![]() 在線段
在線段![]() 的反向延長線上時,且點
的反向延長線上時,且點![]() 分別在直線
分別在直線![]() 的兩側,其他條件不變;
的兩側,其他條件不變;
①請直接寫出![]() 三條線段之間的關系;
三條線段之間的關系;
②若正方形![]() 的邊長為
的邊長為![]() 、對角線
、對角線![]() 相交于點
相交于點![]() ,連接
,連接![]() ,求
,求![]() 的長度.
的長度.
【答案】(1)![]() ;證明見解析;(2)
;證明見解析;(2)![]() ;(3)①
;(3)①![]() ,②
,② ![]() .
.
【解析】
(1)根據SAS證明△ABD≌△ACF,由△ABD≌△ACF的性質和線段的和可得結論;
(2)同理證明△ABD≌△ACF,可得BC⊥CF,由BD=BC+CD,BD=CF,可得新的結論:![]() ;
;
(3)①根據圖3知:DC最長,同理:△DAB≌△FAC,則BD=CF,可得BC=DC-CF;
②先根據正方形的邊長求對角線DF的長,證明∠DCF=90°,根據直角三角形斜邊中線的性質可得OC的長.
證明:![]() ,
,![]() ,
,
![]()
![]() 四邊形
四邊形![]() 是正方形,
是正方形,
![]() ,
,
![]() ,
,![]()
![]()
則在![]() 和
和![]() 中,
中,

![]() ,
,
![]()
![]() ,
,
![]() ;
;
(2)證明:如圖2,
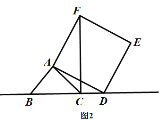
在正方形ADEF中,AD=AF,∠DAF=90°,
∵∠BAC=90°,
∴∠BAC+∠CAD=∠DAF+∠CAD,即∠BAD=∠CAF,
∵∠ABC=45°,
∴∠ACB=180°-∠BAC-∠ABC=45°,
∴∠ABC=∠ACB,
∴AB=AC,
在△ABD與△ACF中,

∴△ABD≌△ACF,
∴∠ACF=∠ABD=45°,BD=CF,
∵∠ACB=45°,
∴∠BCF=∠ACB+∠ACF=90°,
∴BC⊥CF;
∵BD=BC+CD,BD=CF,
∴![]() ;
;
(3)①理由是:如圖3,
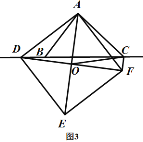
同理得:∠DAB=∠FAC,
與(2)同理,可證△DAB≌△FAC,
∴BD=CF,
∴DC=BD+BC=CF+BC,
∴BC=DC-CF;
![]() ,
,
![]()
![]()
![]() 四邊形
四邊形![]() 是正方形,
是正方形,
![]() ,
,
![]()
![]()
![]() 在
在![]() 和
和![]() 中,
中,

![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是直角三角形.
是直角三角形.
![]() 正方形
正方形![]() 的邊長為
的邊長為![]()
且對角線![]() 相交于點
相交于點![]()
![]()
![]() 為
為![]() 中點.
中點.
![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在一個不透明的袋子中裝有僅顏色不同的10個小球,其中紅球4個,黑球6個.
(1)先從袋子中取出m(m>1)個紅球,再從袋子中隨機摸出1個球,將“摸出黑球”記為事件A,請完成下列表格;
![]()
(2)先從袋子中取出m個紅球,再放入m個一樣的黑球并搖勻,隨機摸出1個黑球的概率等于![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店經銷一種成本為每千克40元的水產品,據市場分析,若按每千克50元銷售,一個月能售出500千克.若銷售價每漲1元,則月銷售量減少10千克.
(1)要使月銷售利潤達到最大,銷售單價應定為多少元?
(2)要使月銷售利潤不低于8000元,請結合圖象說明銷售單價應如何定?
查看答案和解析>>
科目:初中數學 來源: 題型:
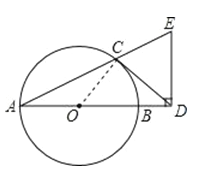
【題目】如圖,AB 是⊙O 的直徑,CD 與⊙O 相切于點 C,與 AB 的延長線交于點 D,DE⊥AD 且與AC 的延長線交于點 E.
(1)求證:DC=DE;
(2)若 AD=2ED,AB=3,求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將平行四邊形ABCD的邊DC延長到點E,使CE=DC,連接AE,交BC于點F.
(1)求證:AC=BE;
(2)若∠AFC=2∠D,連接AC,BE.求證:四邊形ABEC是矩形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,∠BAD=80°,AB的垂直平分線交對角線AC于點F,垂足為E,連接DF,則∠CDF等于()

A.50°B.60°C.70°D.80°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次函數y=kx+b的圖象與反比例函數y=![]() 的圖象交于點A(2,1),B(-1,n)兩點.
的圖象交于點A(2,1),B(-1,n)兩點.
(1)求反比例函數的解析式;
(2)求一次例函數的解析式;
(3)求△AOB的面積.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com