
 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:初中數學 來源: 題型:
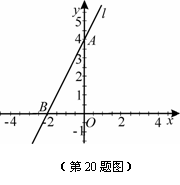
如圖,在平面直角坐標系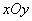 中,直線
中,直線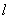 經過
經過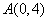 和
和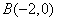 兩點.
兩點.
(1)求直線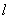 的解析式及原點到直線
的解析式及原點到直線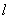 的距離;
的距離;
(2)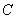 、
、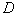 兩點的坐標分別為
兩點的坐標分別為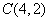 、
、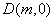 ,且
,且
⊿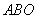 ≌⊿
≌⊿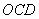 則
則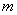 的值為 ;(直接寫出結論)
的值為 ;(直接寫出結論)
(3)若直線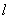 向下平移
向下平移 個單位后經過(2)中的點
個單位后經過(2)中的點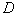 ,求
,求 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
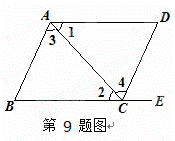
如圖,給出下列條件:①∠1=∠2;②∠3=∠4;③AD∥BE,且∠D=∠B;
④AD∥BE,且 ∠BAD=∠BCD.其中,能推出AB∥DC的條件為( )
∠BAD=∠BCD.其中,能推出AB∥DC的條件為( )
A.① B.② C.②③ D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
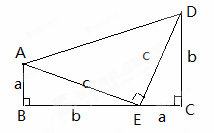
如圖,梯形ABCD是由三個直角三角形拼成的,各直角邊的長度如圖所示。
(1)請你運用兩種方法計算梯形ABCD的面積;
(2)根據(1)的計算,探索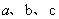 三者之間的關系,并用式子表示出來。
三者之間的關系,并用式子表示出來。
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖①,△ABC的角平分線BD、CE相交于點P.
(1)如果∠A=70°,求∠BPC的度數;
(2)如圖②,過P點作直線MN∥BC,分別交AB和AC于點M和N,試求
∠MPB+∠NPC的度數(用含∠A的代數式表示);
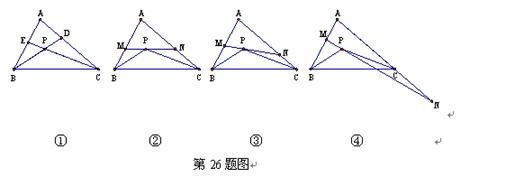
(3)在(2)的條件下,將直線MN繞點P旋轉.
(i)當直線MN與AB、AC的交點仍分別在線段AB和AC上時,如圖③,
試 探索∠MPB、∠NPC、∠A三者之間的數量關系,并說明你的理由;
探索∠MPB、∠NPC、∠A三者之間的數量關系,并說明你的理由;
(ii)當直線MN與AB的交點仍在線段AB上,而與AC的交點在AC的
延長線上時,如圖④,試問(i)中∠MPB、∠NPC、∠A三者之間
的數量關系是否仍然成立?若成立,請說明你的理由;若不成立,請
給出∠MPB、∠NPC、∠A三者之間的數量關系,并說明你的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com