
【題目】已知拋物線y=ax2﹣4a(a>0)與x軸相交于A,B兩點(點A在點B的左側),點P是拋物線上一點,且PB=AB,∠PBA=120°,如圖所示.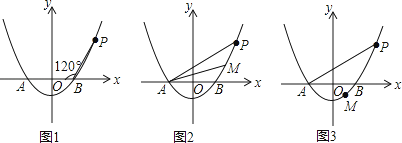
(1)求拋物線的解析式.
(2)設點M(m,n)為拋物線上的一個動點,且在曲線PA上移動.
①當點M在曲線PB之間(含端點)移動時,是否存在點M使△APM的面積為 ![]() ?若存在,求點M的坐標;若不存在,請說明理由.
?若存在,求點M的坐標;若不存在,請說明理由.
②當點M在曲線BA之間(含端點)移動時,求|m|+|n|的最大值及取得最大值時點M的坐標.
【答案】
(1)
解:如圖1
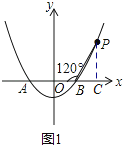 ,
,
令y=0代入y=ax2﹣4a,
∴0=ax2﹣4a,
∵a>0,
∴x2﹣4=0,
∴x=±2,
∴A(﹣2,0),B(2,0),
∴AB=4,
過點P作PC⊥x軸于點C,
∴∠PBC=180°﹣∠PBA=60°,
∵PB=AB=4,
∴cos∠PBC= ![]() ,
,
∴BC=2,
由勾股定理可求得:PC=2 ![]() ,
,
∵OC=OC+BC=4,
∴P(4,2 ![]() ),
),
把P(4,2 ![]() )代入y=ax2﹣4a,
)代入y=ax2﹣4a,
∴2 ![]() =16a﹣4a,
=16a﹣4a,
∴a= ![]() ,
,
∴拋物線解析式為;y= ![]() x2﹣
x2﹣ ![]()
(2)
解:∵點M在拋物線上,
∴n= ![]() m2﹣
m2﹣ ![]() ,
,
∴M的坐標為(m, ![]() m2﹣
m2﹣ ![]() ),
),
①當點M在曲線PB之間(含端點)移動時,
∴2≤m≤4,
如圖2,

過點M作ME⊥x軸于點E,交AP于點D,
設直線AP的解析式為y=kx+b,
把A(﹣2,0)與P(4,2 ![]() )代入y=kx+b,
)代入y=kx+b,
得: ![]() ,
,
解得 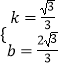
∴直線AP的解析式為:y= ![]() x+
x+ ![]() ,
,
令x=m代入y= ![]() x+
x+ ![]() ,
,
∴y= ![]() m+
m+ ![]() ,
,
∴D的坐標為(m, ![]() m+
m+ ![]() ),
),
∴DM=( ![]() m+
m+ ![]() )﹣(
)﹣( ![]() m2﹣
m2﹣ ![]() )=﹣
)=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]()
![]() ,
,
∴S△APM= ![]() DMAE+
DMAE+ ![]() DMCE
DMCE
= ![]() DM(AE+CE)
DM(AE+CE)
= ![]() DMAC
DMAC
=﹣ ![]() m2+
m2+ ![]() m+4
m+4 ![]()
當S△APM= ![]()
![]() 時,
時,
∴ ![]()
![]() =﹣
=﹣ ![]() m2+
m2+ ![]() m+4
m+4 ![]() ,
,
∴解得m=3或m=﹣1,
∵2≤m≤4,
∴m=3,
此時,M的坐標為(3, ![]() );
);
②當點M在曲線BA之間(含端點)移動時,
∴﹣2≤m≤2,n<0,
當﹣2≤m≤0時,
∴|m|+|n|=﹣m﹣n=﹣ ![]() m2﹣m+
m2﹣m+ ![]() =﹣
=﹣ ![]() (m+
(m+ ![]() )2+
)2+ ![]() ,
,
當m=﹣ ![]() 時,
時,
∴|m|+|n|可取得最大值,最大值為 ![]()
![]() ,
,
此時,M的坐標為(﹣ ![]() ,﹣
,﹣ ![]() ),
),
當0<m≤2時,
∴|m|+|n|=m﹣n=﹣ ![]() m2+m+
m2+m+ ![]() =﹣
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
當m= ![]() 時,
時,
∴|m|+|n|可取得最大值,最大值為 ![]() ,
,
此時,M的坐標為( ![]() ,﹣
,﹣ ![]() ),
),
綜上所述,當點M在曲線BA之間(含端點)移動時,M的坐標為( ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,﹣
,﹣ ![]() )時,|m|+|n|的最大值為
)時,|m|+|n|的最大值為 ![]() .
.
【解析】(1)先求出A、B兩點坐標,然后過點P作PC⊥x軸于點C,根據∠PBA=120°,PB=AB,分別求出BC和PC的長度即可得出點P的坐標,最后將點P的坐標代入二次函數解析式即;(2)①過點M作ME⊥x軸于點E,交AP于點D,分別用含m的式子表示點D、M的坐標,然后代入△APM的面積公式 ![]() DMAC,根據題意列出方程求出m的值;
DMAC,根據題意列出方程求出m的值;
②根據題意可知:n<0,然后對m的值進行分類討論,當﹣2≤m≤0時,|m|=﹣m;當0<m≤2時,|m|=m,列出函數關系式即可求得|m|+|n|的最大值.本題考查二次函數的綜合問題,涉及待定系數法求二次函數解析式,三角形面積公式,二次函最值等知識,要注意將三角形分解成兩個三角形求解;還要注意求最大值可以借助于二次函數的性質.


 精英口算卡系列答案
精英口算卡系列答案 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案科目:初中數學 來源: 題型:
【題目】如圖,將等邊△ABC繞點C順時針旋轉120°得到△EDC,連接AD,BD.則下列結論:
①AC=AD;②BD⊥AC;③四邊形ACED是菱形.
其中正確的個數是( )
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王師傅檢修一條長600米的自來水管道,計劃用若干小時完成,在實際檢修過程中,每小時檢修管道長度是原計劃的1.2倍,結果提前2小時完成任務,王師傅原計劃每小時檢修管道多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某次海上軍事學習期間,我軍為確保△OBC海域內的安全,特派遣三艘軍艦分別在O、B、C處監控△OBC海域,在雷達顯示圖上,軍艦B在軍艦O的正東方向80海里處,軍艦C在軍艦B的正北方向60海里處,三艘軍艦上裝載有相同的探測雷達,雷達的有效探測范圍是半徑為r的圓形區域.(只考慮在海平面上的探測)
(1)若三艘軍艦要對△OBC海域進行無盲點監控,則雷達的有效探測半徑r至少為多少海里?
(2)現有一艘敵艦A從東部接近△OBC海域,在某一時刻軍艦B測得A位于北偏東60°方向上,同時軍艦C測得A位于南偏東30°方向上,求此時敵艦A離△OBC海域的最短距離為多少海里?
(3)若敵艦A沿最短距離的路線以20 ![]() 海里/小時的速度靠近△OBC海域,我軍軍艦B沿北偏東15°的方向行進攔截,問B軍艦速度至少為多少才能在此方向上攔截到敵艦A?
海里/小時的速度靠近△OBC海域,我軍軍艦B沿北偏東15°的方向行進攔截,問B軍艦速度至少為多少才能在此方向上攔截到敵艦A?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,A、B、C、D為矩形的四個頂點,AD=4cm,AB=dcm.動點E、F分別從點D、B出發,點E以1cm/s的速度沿邊DA向點A移動,點F以1cm/s的速度沿邊BC向點C移動,點F移動到點C時,兩點同時停止移動.以EF為邊作正方形EFGH,點F出發xs時,正方形EFGH的面積為ycm2 . 已知y與x的函數圖象是拋物線的一部分,如圖2所示.請根據圖中信息,解答下列問題:
(1)自變量x的取值范圍是;
(2)d= , m= , n=;
(3)F出發多少秒時,正方形EFGH的面積為16cm2?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在梯形ABCD中,AD∥BC,∠A=60°,動點P從A點出發,以1cm/s的速度沿著A→B→C→D的方向不停移動,直到點P到達點D后才停止.已知△PAD的面積S(單位:cm2)與點P移動的時間(單位:s)的函數如圖②所示,則點P從開始移動到停止移動一共用了秒(結果保留根號).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com