
如圖,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=DC,點E在對角線BD上,作∠ECF=90°,連接DF,且滿足CF=EC.
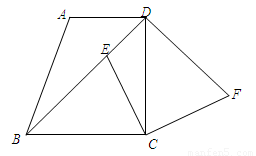
(1)求證:BD⊥DF;
(2)當 時,試判斷四邊形DECF的形狀,并說明理由.
時,試判斷四邊形DECF的形狀,并說明理由.
(1)由 可得
可得 ,再結合
,再結合 即可證得
即可證得 ≌
≌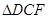 ,則
,則 ,由
,由 可得
可得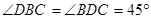 ,即可得到
,即可得到 ,從而可以證得結論;
,從而可以證得結論;
(2)由 ,可得
,可得 ,再結合
,再結合 可證得
可證得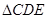 ∽
∽ ,即可得到
,即可得到 ,再結合
,再結合 可得四邊形
可得四邊形 是矩形,從而可以作出判斷.
是矩形,從而可以作出判斷.
【解析】
試題分析:(1)由 可得
可得 ,再結合
,再結合 即可證得
即可證得 ≌
≌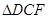 ,則
,則 ,由
,由 可得
可得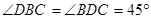 ,即可得到
,即可得到 ,從而可以證得結論;(2)正方形
,從而可以證得結論;(2)正方形
(1)∵ ,
,
∴
∵ ,
,
∴ ≌
≌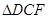
∴
∵ ,
,
∴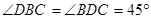
∴ ,
,
∴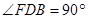
∴ ;
;
(2)四邊形 是正方形
是正方形
∵ ,
,
∴ ,
,
∴
∵ ∴
∴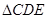 ∽
∽
∴
∵ ,
,
∴四邊形 是矩形
是矩形
∵ ,
,
∴四邊形 是正方形.
是正方形.
考點:全等三角形的判定和性質,相似三角形的判定和性質,矩形、正方形的判定
點評:全等三角形的判定和性質是初中數學的重點,貫穿于整個初中數學的學習,是中考中比較常見的知識點,一般難度不大,需熟練掌握.


 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案科目:初中數學 來源: 題型:
 如圖,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD為直徑的半圓O切AB于點E,這個梯形的面積為21cm2,周長為20cm,那么半圓O的半徑為( )
如圖,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD為直徑的半圓O切AB于點E,這個梯形的面積為21cm2,周長為20cm,那么半圓O的半徑為( )| A、3cm | B、7cm | C、3cm或7cm | D、2cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com