
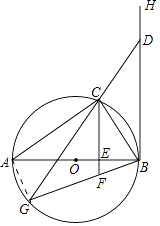
【題目】已知:AB為⊙O的直徑,C是⊙O上一點,如圖,AB=12,BC=4 ![]() .BH與⊙O相切于點B,過點C作BH的平行線交AB于點E.
.BH與⊙O相切于點B,過點C作BH的平行線交AB于點E.
(1)求CE的長;
(2)延長CE到F,使EF= ![]() ,連接BF并延長BF交⊙O于點G,求BG的長;
,連接BF并延長BF交⊙O于點G,求BG的長;
(3)在(2)的條件下,連接GC并延長GC交BH于點D,求證:BD=BG.
【答案】
(1)
解:∵BH與⊙O相切于點B,
∴AB⊥BH,
∵BH∥CE,
∴CE⊥AB,
∵AB是直徑,
∴∠CEB=∠ACB=90°,
∵∠CBE=∠ABC,
∴△ABC∽△CBE,
∴ ![]() =
= ![]() ,
,
∵AC= ![]() =4
=4 ![]() ,
,
∴CE=4 ![]()
(2)
解:連接AG.
∵∠FEB=∠ACB=90°,∠EBF=∠ABC,
∴△ABG∽△FBE,
∴ ![]() =
= ![]() ,
,
∵BE= ![]() =4,
=4,
∴BF= ![]() =3
=3 ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BG=8 ![]()
(3)
解:易知CF=4 ![]() +
+ ![]() =5
=5 ![]() ,
,
∴GF=BG﹣BF=5 ![]() ,
,
∴CF=GF,
∴∠FCG=∠FGC,
∵CF∥BD,
∴∠GCF=∠BDG,
∴∠BDG=∠BGD,
∴BG=BD.
【解析】(1)只要證明△ABC∽△CBE,可得 ![]() =
= ![]() ,由此即可解決問題.(2)連接AG.只要證明△ABG∽△FBE,可得
,由此即可解決問題.(2)連接AG.只要證明△ABG∽△FBE,可得 ![]() =
= ![]() ,由BE=
,由BE= ![]() =4,再求出BF,即可解決問題.(3)通過計算首先證明CF=FG,推出∠FCG=∠FGC,由CF∥BD,推出∠GCF=∠BDG,推出∠BDG=∠BGD即可證明.
=4,再求出BF,即可解決問題.(3)通過計算首先證明CF=FG,推出∠FCG=∠FGC,由CF∥BD,推出∠GCF=∠BDG,推出∠BDG=∠BGD即可證明.
【考點精析】解答此題的關鍵在于理解勾股定理的概念的相關知識,掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2,以及對切線的性質定理的理解,了解切線的性質:1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑.


科目:初中數學 來源: 題型:
【題目】一個不透明袋子中有1個紅球,1個綠球和n個白球,這些球除顏色外無其他差別.
(1)當n=1時,從袋中隨機摸出1個球,摸到紅球和摸到白球的可能性是否相同?(在答題卡相應位置填“相同”或“不相同”);
(2)從袋中隨機摸出一個球,記錄其顏色,然后放回,大量重復該實驗,發現摸到綠球的頻率穩定于0.25,則n的值是
(3)在一個摸球游戲中,所有可能出現的結果如下:
根據樹狀圖呈現的結果,求兩次摸出的球顏色不同的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
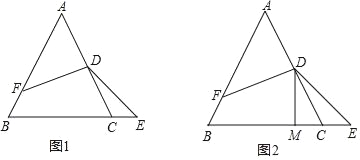
【題目】如圖1,等邊△ABC中,D為AC中點,∠EDF=120°,DF交AB于F點,且AF=nBF(n為常數,且n>1).
(1)求證:DF=DE;
(2)如圖1,求證:AF﹣CE=![]() AB;
AB;
(3)如圖2,當n= 時,過D作DM⊥BC于M點,C為EM的中點.
查看答案和解析>>
科目:初中數學 來源: 題型:
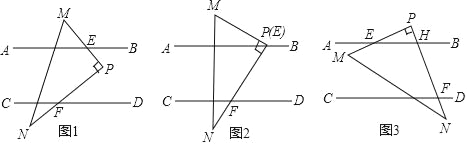
【題目】問題情境:已知:如圖1,直線AB∥CD,現將直角三角板△PMN放入圖中,其中∠MPN=90°,點P始終在直線MN右側.PM交AB于點E,PN交CD于點F,試探究:∠PFD與∠AEM的數量關系.
(1)特例如圖2,當點P在直線AB上(即點E與點P重合)時,直接寫出∠PFD與∠AEM的數量關系,不必證明;
(2)類比探究:如圖1,當點P在AB與CD之間時,猜想∠PFD與∠AEM的數量關系,并說明理由;
(3)拓展延伸:如圖3,當點P在直線AB的上方時,PN交AB于點H,其他條件不變,猜想∠PFD與∠AEM的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某市市民晚飯后1小時內的生活方式,調查小組設計了“閱讀”、“鍛煉”、“看電視”和“其它”四個選項,用隨機抽樣的方法調查了該市部分市民,并根據調查結果繪制成如下統計圖.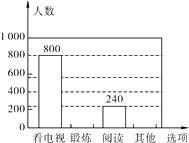
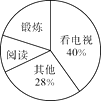
根據統計圖所提供的信息,解答下列問題:
(1)本次共調查了名市民;
(2)補全條形統計圖;
(3)該市共有480萬市民,估計該市市民晚飯后1小時內鍛煉的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某科技有限公司準備購進A和B兩種機器人來搬運化工材料,已知購進A種機器人2個和B種機器人3個共需16萬元;購進A種機器人3個和B種機器人2個共需14萬元.請解答下列問題:
(1)求A , B兩種機器人每個的進價;
(2)已知該公司購買B種機器人的個數比購買A種機器人的個數的2倍多4個,如果需要購買A、B兩種種機器人的總個數不少于28個,且該公司購買的A、B兩種種機器人的總費用不超過106萬元,那么該公司有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知,BC∥OA,∠B=∠A=100°,試回答下列問題:

(1)如圖①,求證:OB∥AC.
(2)如圖②,若點E、F在線段BC上,且滿足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度數.
(3)在(2)的條件下,若平行移動AC,如圖③,那么∠OCB:∠OFB的值是否隨之發生變化?若變化,試說明理由;若不變,求出這個比值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com