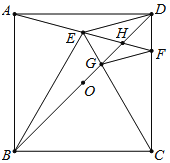
【題目】如圖，正方形ABCD中，O為BD中點，以BC為邊向正方形內作等邊
，連接并延長AE交CD于F，連接BD分別交CE、AF于G、H，下列結論：
；
；
；
；
：
，其中正確的結論有
A. 
B. 
C. 
D. 
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，
，連結AC，過點C作直線l∥AB，點P是直線l上的一個動點，直線PA與⊙O交于另一點D，連結CD，設直線PB與直線AC交于點E．
（1）求∠BAC的度數；
（2）當點D在AB上方，且CD⊥BP時，求證：PC=AC；
（3）在點P的運動過程中
①當點A在線段PB的中垂線上或點B在線段PA的中垂線上時，求出所有滿足條件的∠ACD的度數；
②設⊙O的半徑為6，點E到直線l的距離為3，連結BD，DE，直接寫出△BDE的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】江南農場收割小麥，已知1臺大型收割機和3臺小型收割機1小時可以收割小麥1.4公頃，2臺大型收割機和5臺小型收割機1小時可以收割小麥2.5公頃．
（1）每臺大型收割機和每臺小型收割機1小時收割小麥各多少公頃？
（2）大型收割機每小時費用為300元，小型收割機每小時費用為200元，兩種型號的收割機一共有10臺，要求2小時完成8公頃小麥的收割任務，且總費用不超過5400元，有幾種方案？請指出費用最低的一種方案，并求出相應的費用．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，O為菱形ABCD對角線上一點，以點O為圓心，OA長為半徑的⊙O與BC相切于點M．
（1）求證：CD與⊙O相切；
（2）若菱形ABCD的邊長為2，∠ABC＝60°，求⊙O的半徑．
查看答案和解析>>
科目：初中數學 來源： 題型：
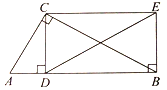
【題目】如圖，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足為D ，BE⊥AB，垂足為B，BE=CD連接CE，DE.
（1）求證：四邊形CDBE是矩形
（2）若AC=2 ，∠ABC=30°，求DE的長
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某同學準備購買筆和本子送給農村希望小學的同學，在市場上了解到某種本子的單價比某種筆的單價少4元，且用30元買這種本子的數量與用50元買這種筆的數量相同．
（1）求這種筆和本子的單價；
（2）該同學打算用自己的100元壓歲錢購買這種筆和本子，計劃100元剛好用完，并且筆和本子都買，請列出所有購買方案．
查看答案和解析>>
科目：初中數學 來源： 題型：
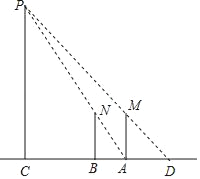
【題目】甲和乙兩位同學想測量一下廣場中央的照明燈P的高度，如圖，當甲站在A處時，乙測得甲的影子長AD正好與他的身高AM相等，接著甲沿AC方向繼續向前走，走到點B處時，甲的影子剛好是線段AB，此時測得AB的長為1.2m．已知甲直立時的身高為1.8m，求照明燈的高CP的長．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
