
【題目】如圖,在邊長為12cm的等邊三角形ABC中,點P從點A開始沿AB邊向點B以每秒鐘1cm的速度移動,點Q從點B開始沿BC邊向點C以每秒鐘2cm的速度移動。若P、Q分別從A、B同時出發,其中任意一點到達目的地后,兩點同時停止運動,求: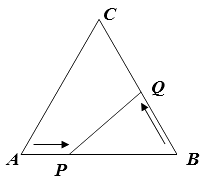
(1)經過6秒后,BP= cm,BQ=cm;
(2)經過幾秒后,△BPQ是直角三角形?
(3)經過幾秒△BPQ的面積等于 ![]() cm2 ?
cm2 ?
【答案】
(1)6;12
(2)
∵△ABC是等邊三角形,
∴AB=AC=12cm,∠A=∠B=∠C=60°,
當∠PQB=90°時,
∴∠BPQ=30°,
∴BP=2BQ
∵BP=12-x,BQ=2x,
∴12-x=2×2x,
∴ ![]()
當∠QPB=90°時,
∴∠PQB=30°,
∴BQ=2PB,
∴2x=2(12-x),
x=6
答:6秒或 ![]() 秒時,△BPQ是直角三角形;
秒時,△BPQ是直角三角形;
(3)
作QD⊥AB于D,
∴∠QDB=90°,
∴∠DQB=30°,
∴DB =0.5 BQ=x,
在Rt△DBQ中,由勾股定理,得
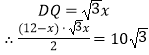
解得;x1=10,x2=2,
∵x=10時,2x>12,故舍去
∴x=2.
答:經過2秒△BPQ的面積等于 ![]() cm2
cm2
【解析】(1)解:由題意,得
AP=6cm,BQ=12cm.
∵△ABC是等邊三角形
∴AB=BC=12cm,
∴BP=12-6=6cm.
【考點精析】根據題目的已知條件,利用等邊三角形的性質和勾股定理的概念的相關知識可以得到問題的答案,需要掌握等邊三角形的三個角都相等并且每個角都是60°;直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】小紅的媽媽買了4筐白菜,以每筐25千克為標準,超過的千克數記為正數,不足的千克數記為負數,稱重后的記錄分別為+0.25,-1, +0.5, 0.75。小紅快速準確地算出了4筐白菜的總質量為( )
A. 一1千克 B. 1千克 C. 99千克 D. 101千克
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平行四邊形的周長為24,相鄰兩邊的差為2,則平行四邊形的各邊長為( ).
A. 4,4,8,8 B. 5,5,7,7 C. 5.5,5.5,6.5,6.5 D. 3,3,9,9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數y=x+2與y=-2x+6的圖象相交于點A,函數y=-2x+6的圖象分別交x軸、y軸于點B、C,函數y=x+2的圖象分別與x軸、y軸交于點E、D.
(1)求點A的坐標;
(2)求△ABE的面積.
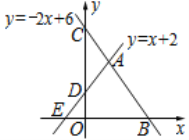
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張勤同學的父母在外打工,家中只有年邁多病的奶奶.星期天早上,李老師從家中出發步行前往張勤家家訪.6分鐘后,張勤從家出發騎車到相距1200米的藥店給奶奶買藥,停留14分鐘后以相同的速度按原路返回,結果與李老師同時到家.張勤家、李老師家、藥店都在東西方向筆直大路上,且藥店在張勤家與李老師家之間.在此過程中設李老師出發t(0≤t≤32)分鐘后師生二人離張勤家的距離分別為S1、S2 . S1與t之間的函數關系如圖所示,請你解答下列問題: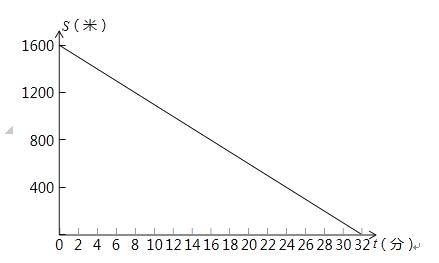
(1)李老師步行的速度為。
(2)求S2與t之間的函數關系式,并在如圖所示的直角坐標系中畫出其函數圖象;
(3)張勤出發多長時間后在途中與李老師相遇?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com