
【題目】如圖,拋物線y=ax2+bx+c過原點O、點A (2,﹣4)、點B (3,﹣3),與x軸交于點C,直線AB交x軸于點D,交y軸于點E.
(1)求拋物線的函數表達式和頂點坐標;
(2)直線AF⊥x軸,垂足為點F,AF上取一點G,使△GBA∽△AOD,求此時點G的坐標;
(3)過直線AF左側的拋物線上點M作直線AB的垂線,垂足為點N,若∠BMN=∠OAF,求直線BM的函數表達式.
【答案】解:(1)∵將原點O、點B、點C的坐標代入得: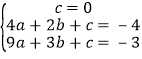 ,解得:a=1,b=﹣4,c=0,
,解得:a=1,b=﹣4,c=0,
∴拋物線的解析式為y=x2﹣4x.
(2)設直線AB的解析式為y=kx+b.
∵將點A(2,﹣4)、B(3,﹣3)代入得![]() ,解得:k=1,b=﹣6,
,解得:k=1,b=﹣6,
∴直線AB的解析式為y=x﹣6.
∵令y=0得x﹣6=0,解得:x=6,
∴D(6,0).
∴OD=6.
∵AF⊥x軸,(2,﹣4),
∴F(2,0).
∴AF=4,DF=4.
∴AF=DF.
∴∠GAB=∠ODA.
∴當![]() 時,△GBA∽△AOD.
時,△GBA∽△AOD.
∵由兩點間的距離公式可知AB=![]() =
=![]() ,AD=
,AD=![]() =4
=4![]() ,
,
∴![]() ,解得;AG=
,解得;AG=![]() .
.
∴G(2,﹣![]() ).
).
(3)如圖1所示:BM與AF的交點記為G.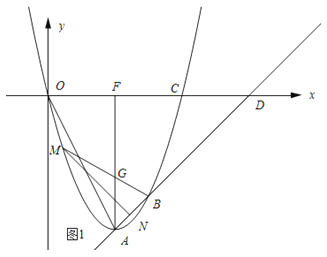
∵∠BMN=∠OAF,∠A=∠ODA,
∴△GBA∽△AOD.
∴![]() ,即
,即![]() ,解得;AG=
,解得;AG=![]() .
.
∴G(2,﹣![]() ).
).
設直線BM的解析式為y=kx+b.
∵將點B、G的坐標代入得: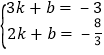 ,解得:k=﹣
,解得:k=﹣![]() ,b=﹣2.
,b=﹣2.
∴直線BM的解析式為y=﹣![]() X﹣2.
X﹣2.
如圖2所示:MB與x交點記為G.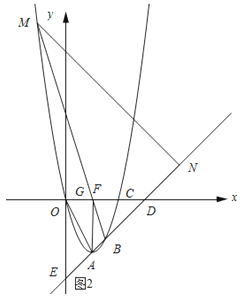
BD=AD﹣AB=4![]() ﹣
﹣![]() =3
=3![]() .
.
∵∠BMN=∠OAF,∠GDB=∠ODA,
∴△FBD∽△AOD.
∴![]() ,即
,即![]() ,解得DG=4.
,解得DG=4.
∴點G的坐標為(2,0).
設直線BM的解析式為y=kx+b.
∵將點B和點G的坐標代入得:![]() ,解得k=﹣3,b=6.
,解得k=﹣3,b=6.
∴直線BM的解析式為y=﹣3x+6.
綜上所述,直線MB的解析式為y=-![]() x﹣2或y=﹣3x+6.
x﹣2或y=﹣3x+6.
【解析】(1)將原點O、點B、點C的坐標代入求得a、b、c的值即可;
(2)先求得直線AB的解析式,然后可求得點D的坐標,于是得到AF=DF,由兩點間的距離公式可求得AB、AD的長,由等腰三角形的性質可證明∠GAB=∠ODA,故此![]() 時,△GBA∽△AOD.接下來依據關系式可求得AG的長,從而可求得點G的坐標;
時,△GBA∽△AOD.接下來依據關系式可求得AG的長,從而可求得點G的坐標;
(3)如圖1所示:BM與AF的交點記為G.先證明△GBA∽△AOD,由相似三角形的性質可求得AG的長,于是得到點G的坐標,然后依據待定系數法可求得BM的解析式;如圖2所示:MB與x交點記為G.先證明△FBD∽△AOD,由相似三角形的性質可求得DG的長,從而得到點G的坐標,然后依據待定系數法可求得MB的解析式


科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=90°,∠A=30°.分別以頂點A,B為圓心,大于![]() AB的長為半徑作弧,兩弧在直線AB兩側分別交于M,N兩點,過M,N作直線交AB于點P,交AC于點D,連結BD.下列結論中,錯誤的是( )
AB的長為半徑作弧,兩弧在直線AB兩側分別交于M,N兩點,過M,N作直線交AB于點P,交AC于點D,連結BD.下列結論中,錯誤的是( )
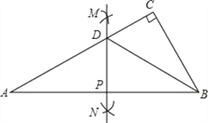
A. 直線AB是線段MN的垂直平分線 B. CD=![]() AD
AD
C. BD平分∠ABC D. S△APD=S△BCD
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,已知AB∥CD,點E、F分別是AB、CD上的點,點P是兩平行線之間的一點,設∠AEP=α,∠PFC=β,在圖①中,過點E作射線EH交CD于點N,作射線FI,延長PF到G,使得PE、FG分別平分∠AEH、∠DFl,得到圖②.
(1)在圖①中,過點P作PM∥AB,當α=20°,β=50°時,∠EPM= 度,∠EPF= 度;
(2)在(1)的條件下,求圖②中∠END與∠CFI的度數;
(3)在圖②中,當FI∥EH時,請直接寫出α與β的數量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
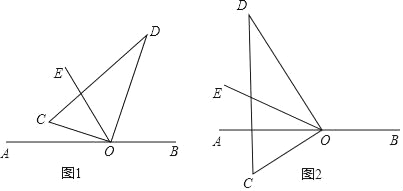
【題目】如圖,直角三角板的直角頂點O在直線AB上,OC,OD是三角板的兩條直角邊,OE平分∠AOD.
(1)若∠COE=20°,則∠BOD= ;若∠COE=α,則∠BOD= (用含α的代數式表示)
(2)當三角板繞O逆時針旋轉到圖2的位置時,其它條件不變,試猜測∠COE與∠BOD之間有怎樣的數量關系?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年以來,國務院連續發布了《關于加快構建大眾創業萬眾創新支撐平臺的指導意見》等一系列支持性政策,各地政府高度重視、積極響應,中國掀起了大眾創業萬眾創新的新浪潮.某創新公司生產營銷A、B兩種新產品,根據市場調研,發現如下信息:
信息1:銷售A種產品所獲利潤y(萬元)與所售產品x(噸)之間存在二次函數關系y=ax2+bx,當x=1時,y=7;當x=2時,y=12.
信息2:銷售B種產品所獲利潤y(萬元)與所售產品x(噸)之間存在正比例函數關系y=2x.
根據以上信息,解答下列問題:
(1)求a,b的值;
(2)該公司準備生產營銷A、B兩種產品共10噸,請設計一個生產方案,使銷售A、B兩種產品獲得的利潤之和最大,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=![]() x+6與y軸交于點A,與x軸交于點B,點M是射線AB上一動點(點M不與點A、B重合),以點M為圓心,MA長為半徑的圓交y軸于另一點C,直線MC與x軸交于點D,點E是線段BD的中點,射線ME交⊙M于點F,連接OF.
x+6與y軸交于點A,與x軸交于點B,點M是射線AB上一動點(點M不與點A、B重合),以點M為圓心,MA長為半徑的圓交y軸于另一點C,直線MC與x軸交于點D,點E是線段BD的中點,射線ME交⊙M于點F,連接OF.
(1)若MA=2,求C點的坐標;
(2)若D點的坐標為(4,0),求MC的長;
(3)當OF=MA時,直接寫出點M的坐標.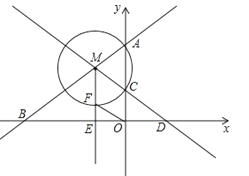
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某探測隊在地面A、B兩處均探測出建筑物下方C處有生命跡象,已知探測線與地面的夾角分別是25°和60°,且AB=4米,求該生命跡象所在位置C的深度.(結果精確到1米.參考數據:sin25°≈0.4,cos25°≈0.9,tan25°≈0.5,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知頂點為(﹣3,﹣6)的拋物線y=ax2+bx+c經過點A,點(﹣2,m)和(﹣5,n)在該拋物線上,則下列結論中不正確的是( )
A.![]() >4ac
>4ac
B.m>n
C.方程a![]() +bx+c=﹣4的兩根為﹣5或﹣1
+bx+c=﹣4的兩根為﹣5或﹣1
D.a![]() +bx+c≥﹣6
+bx+c≥﹣6
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com