
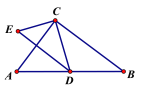
【題目】如圖,已知在Rt△ABC與Rt△ECD中,∠ACB=∠ECD=90°,CD為Rt△ABC斜邊上的中線,且ED∥BC.
(1)求證:△ABC∽△EDC;
(2)若CE=3,CD=4,求CB的長.
【答案】(1)見詳解;(2) ![]() .
.
【解析】
(1)根據直角三角形的性質得到CD=BD,由等腰三角形的性質得到∠DCB=∠B,根據平行線的性質得到∠EDC=∠BCD,等量代換得到∠B=∠EDC,根據相似三角形的判定定理即可得到結論;
(2)根據勾股定理得到DE= ![]() =5,由直角三角形的性質得到AB=2CD=8,根據相似三角形的性質即可得到結論.
=5,由直角三角形的性質得到AB=2CD=8,根據相似三角形的性質即可得到結論.
(1)證明:
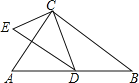
∵在Rt△ABC,CD為Rt△ABC斜邊上的中線,
∴CD=BD,
∴∠DCB=∠B,
∵ED∥BC,
∴∠EDC=∠BCD,
∴∠B=∠EDC,
∵∠ACB=∠ECD=90°,
∴△ABC∽△EDC;
(2)解:∵∠DCE=90°,CE=3,CD=4,
∴DE= ![]() =5,
=5,
∵在Rt△ABC,CD為Rt△ABC斜邊上的中線,
∴AB=2CD=8,
∵△ABC∽△EDC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
=![]() ,
,
∴BC=![]() .
.


科目:初中數學 來源: 題型:
【題目】已知函數y=![]() (x>0)的圖象與一次函數y=ax﹣2(a≠0)的圖象交于點A(3,n).
(x>0)的圖象與一次函數y=ax﹣2(a≠0)的圖象交于點A(3,n).
(1)求實數a的值;
(2)設一次函數y=ax﹣2(a≠0)的圖象與y軸交于點B,若點C在y軸上,且S△ABC=2S△AOB,求點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線y=﹣3x+3與x軸、y軸分別交于A、B兩點,以AB為邊在第一象限作正方形ABCD沿x軸負方向平移a個單位長度后,點C恰好落在雙曲線上,則a的值是 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等腰三角形ABC中,AB=CB=5,AC=8,P為AC邊上一動點,PQ⊥AC,PQ與△ABC的腰交于點Q,連結CQ,設AP為x,△CPQ的面積為y,則y關于x的函數關系的圖象大致是( )
A.  B.
B. 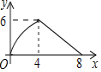 C.
C. 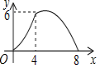 D.
D. 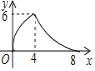
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場開展購物抽獎活動,抽獎箱中有3個形狀、大小和質地等完全相同的小球,分別標有數字1、2、3.顧客從中隨機摸出一個小球,然后放回箱中,再隨機摸出一個小球.
(1)利用樹形圖法或列表法(只選其中一種),表示摸出小球可能出現的所有結果;
(2)若規定:兩次摸出的小球的數字之積為9,則為一等獎;數字之積為6,則為二等獎;數字之積為2或4,則為三等獎.請你分別求出顧客抽中一等獎、二等獎、三等獎的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若反比例函數y=![]() (k≠0)的圖象過點(2,1),則這個函數的圖象還經過的點是( )
(k≠0)的圖象過點(2,1),則這個函數的圖象還經過的點是( )
A. (﹣2,1) B. (﹣l,2) C. (﹣2,﹣1) D. (1,﹣2)
查看答案和解析>>
科目:初中數學 來源: 題型:
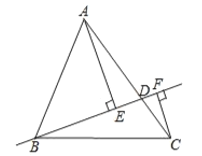
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,點
,點![]() 是線段
是線段![]() 上任意一點,分別過點
上任意一點,分別過點![]() 、
、![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() 、
、![]() ,
,![]() ,
,![]() ,則
,則![]() 的最大值是______________,最小值是______________.
的最大值是______________,最小值是______________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC中,AB=AC,以AB為直徑的⊙O交BC于點D,交AC于點E.
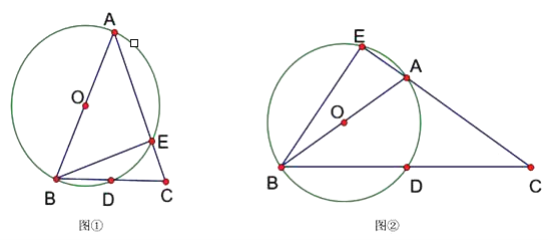
(1)當∠BAC為銳角時,如圖①,求證:∠CBE=![]() ∠BAC;
∠BAC;
(2)當∠BAC為鈍角時,如圖②,CA的延長線與⊙O相交于點E,(1)中的結論是否仍然成立?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com