
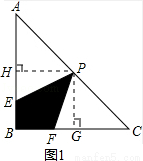
如圖,在等腰直角△ABC中,∠ABC=90°,AB=BC=4,P為AC中點,E為AB邊上一動點,F為BC邊上一動點,且滿足條件∠EPF=45°,記四邊形PEBF的面積為S1;
(1)求證:∠APE=∠CFP;
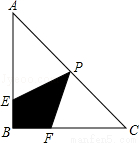
(2)記△CPF的面積為S2,CF=x,y=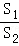 .
.
①求y關于x的函數解析式和自變量的取值范圍,并求y的最大值.
②在圖中作四邊形PEBF關于AC的對稱圖形,若它們關于點P中心對稱,求y的值.
(1)見解析;
(2)①則y關于x的函數解析式為:y=﹣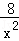 +
+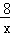 ﹣1,(2≤x≤4),y的最大值為1;
﹣1,(2≤x≤4),y的最大值為1;
②圖見解析, y=2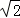 ﹣2.
﹣2.
【解析】
試題分析:(1)分別證出∠APE+∠FPC=∠CFP+∠FPC=135°,即可得出∠APE=∠CFP;
(2)①先證出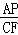 =
=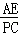 ,再根據AP=CP=2
,再根據AP=CP=2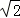 ,得出AE=
,得出AE=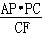 =
= ,過點P作PH⊥AB于點H,PG⊥BC于點G,求出S△APE=
,過點P作PH⊥AB于點H,PG⊥BC于點G,求出S△APE=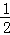 PH•AE=
PH•AE= ,S2=S△PCF=
,S2=S△PCF=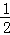 CF×PG=x,再根據S1=S△ABC﹣S△APE﹣S△PCF求出S1=8﹣
CF×PG=x,再根據S1=S△ABC﹣S△APE﹣S△PCF求出S1=8﹣ ﹣x,再代入y=
﹣x,再代入y=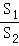 得出y=﹣8(
得出y=﹣8( ﹣
﹣ )2+1,最后根據2≤x≤4,得出
)2+1,最后根據2≤x≤4,得出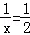 時,y取得最大值,最后將x=2代入y=
時,y取得最大值,最后將x=2代入y=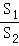 即可求出y最大=1.
即可求出y最大=1.
②根據圖中兩塊陰影部分圖形關于點P成中心對稱,得出陰影部分圖形自身關于直線BD對稱,AE=FC,從而得出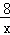 =x,求出x=2
=x,求出x=2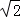 ,最后把
,最后把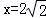 代入y=﹣
代入y=﹣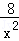 +
+ ﹣1即可.
﹣1即可.
試題解析:(1)∵∠EPF=45°,
∴∠APE+∠FPC=180°﹣45°=135°;
在等腰直角△ABC中,∠PCF=45°,
則∠CFP+∠FPC=180°﹣45°=135°,
∴∠APE=∠CFP.
(2)①∵∠APE=∠CFP,且∠FCP=∠PAE=45°,
∴△APE∽△CFP,
則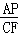 =
=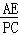 .
.
在等腰直角△ABC中,AC=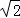 AB=4
AB=4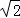 ,
,
又∵P為AC的中點,則AP=CP=2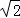 ,
,
∴AE=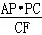 =
=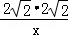 =
=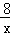 .
.
如圖1,過點P作PH⊥AB于點H,PG⊥BC于點G,
P為AC中點,則PH∥BC,且PH= BC=2,同理PG=2.
BC=2,同理PG=2.
S△APE= PH•AE=
PH•AE= ×2×
×2×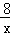 =
=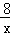 ,
,
S2=S△PCF= CF×PG=
CF×PG= ×x×2=x,
×x×2=x,
∴S1=S△ABC﹣S△APE﹣S△PCF= ×4×4﹣
×4×4﹣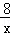 ﹣x=8﹣
﹣x=8﹣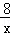 ﹣x,
﹣x,
∴y=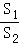 =
= =﹣
=﹣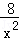 +
+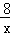 ﹣1=﹣8(
﹣1=﹣8( ﹣
﹣ )2+1,
)2+1,
∵E在AB上運動,F在BC上運動,且∠EPF=45°,
∴2≤x≤4.
即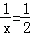 時,y取得最大值.
時,y取得最大值.
而x=2在x的取值范圍內,將x=2代入y=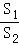 =﹣8(
=﹣8( ﹣
﹣ )2+1,得y最大=1.
)2+1,得y最大=1.
則y關于x的函數解析式為:y=﹣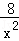 +
+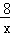 ﹣1,(2≤x≤4),y的最大值為1.
﹣1,(2≤x≤4),y的最大值為1.
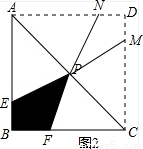
②如圖2所示:
圖中兩塊陰影部分圖形關于點P成中心對稱,則陰影部分圖形自身關于直線BD對稱,
此時EB=BF,即AE=FC,
則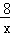 =x,
=x,
解得x1=2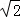 ,x2=﹣2
,x2=﹣2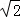 (舍去),
(舍去),
將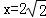 代入y=﹣
代入y=﹣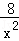 +
+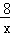 ﹣1,得y=2
﹣1,得y=2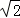 ﹣2.
﹣2.
考點:幾何變換綜合題.


 陽光課堂課時作業系列答案
陽光課堂課時作業系列答案科目:初中數學 來源:2013-2014學年上海市普陀區中考二模數學試卷(解析版) 題型:選擇題
一個不透明的盒子中裝有2個白球,5個紅球和8個黃球,這些球除顏色外,沒有任何其他區別,現從這個盒子中隨機摸出一個球,摸到紅球的概率為( )
A. 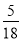 B.
B.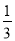 C.
C.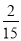 D.
D.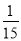
查看答案和解析>>
科目:初中數學 來源:2013-2014學年上海市徐匯區中考二模數學試卷(解析版) 題型:選擇題
“大衣哥”朱之文是從“我是大明星”這個舞臺走出來的民間藝人.受此影響,賣豆腐的老張也來參加節目的海選,當天共有15位選手參加決逐爭取8個晉級名額.已知他們的分數互不相同,老張要判斷自己是否能夠晉級,只要知道下列15名選手成績統計量中的( )
A.眾數 B.方差 C.中位數 D.平均數
查看答案和解析>>
科目:初中數學 來源:2013-2014學年安徽省安慶市中考二模數學試卷(解析版) 題型:解答題
如圖,方格紙中的每個小方格都是邊長為1個單位長度的正方形,每個小正方形的頂點叫格點,△ABC的頂點均在格點上,請按要求完成下列步驟:
(1)先將△ABC向右平移3個單位后得到△A1B1C1,再將△A1B1C1繞點B1按逆時針方向旋轉90°后得到△A2B1C2;試在正方形網格中畫出上述二次變換所得到的圖形;
(2)求線段A1C1旋轉得到A2C2的過程中,線段A1C1所掃過的面積.

查看答案和解析>>
科目:初中數學 來源:2016屆初中數學湘教版七年級上第4章練習卷(解析版) 題型:解答題
有一火車要以每分鐘600米的速度過完第一、第二兩座鐵橋,過第二座鐵橋比過第一座鐵橋多5秒時間,又知第二座鐵橋的長度比第一座鐵橋長度的2倍短50米,試求兩座鐵橋的長分別為多少.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com