解:(1)設F(x,y),(x>0,y>0),則OC=x,CF=y,
∴S
△OCF=

xy=

,
∴xy=2

,
∴k=2

,
∴反比例函數解析式為y=
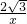
(x>0);
(2)該圓與y軸相離,
理由為:過點E作EH⊥x軸,垂足為H,過點E作EG⊥y軸,垂足為G,
在△AOB中,OA=AB=4,∠AOB=∠ABO=∠A=60°,
設OH=m,則tan∠AOB=
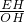
=

,
∴EH=

m,OE=2m,
∴E坐標為(m,

m),
∵E在反比例y=
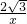
圖象上,
∴

m=
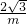
,
∴m
1=

,m
2=-

(舍去),
∴OE=2

,EA=4-2

,EG=

,
∵4-2

<

,
∴EA<EG,
∴以E為圓心,EA垂為半徑的圓與y軸相離;
(3)存在.
假設存在點F,使AE⊥FE,
過E點作EH⊥OB于點H,設BF=x.
∵△AOB是等邊三角形,
∴AB=OA=OB=4,∠AOB=∠ABO=∠A=60°,
∴BC=FB•cos∠FBC=

x,FC=FB•sin∠FBC=

x,
∴AF=4-x,OC=OB-BC=4-

x,
∵AE⊥FE,
∴AE=AF•cosA=2-

x,
∴OE=OA-AE=

x+2,
∴OH=OE•cos∠AOB=

x+1,EH=OE•sin∠AOB=

x+

,
∴E(

x+1,

x+

),F(4-

x,

x),
∵E、F都在雙曲線y=

的圖象上,
∴(

x+1)(

x+

)=(4-

x)•

x,
解得:x
1=4,x
2=

,
當BF=4時,AF=0,
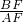
不存在,舍去;
當BF=

時,AF=

,BF:AF=1:4.
分析:(1)設F(x,y),得到OC=x與CF=y,表示出三角形OCF的面積,求出xy的值,即為k的值,進而確定出反比例解析式;
(2)過E作EH垂直于x軸,EG垂直于y軸,設OH為m,利用等邊三角形的性質及銳角三角函數定義表示出EH與OE,進而表示出E的坐標,代入反比例解析式中求出m的值,確定出EG,OE,EH的長,根據EA與EG的大小關系即可對于圓E與y軸的位置關系作出判斷;
(3)過E作EH垂直于x軸,設FB=x,利用等邊三角形的性質及銳角三角函數定義表示出FC與BC,進而表示出AF與OC,表示出AE與OE的長,得出OE與EH的長,表示出E與F坐標,根據E與F都在反比例圖象上,得到橫縱坐標乘積相等列出方程,求出方程的解得到x的值,即可求出BF與FA的比值.
點評:此題屬于反比例函數綜合題,涉及的知識有:反比例函數的圖象與性質,坐標與圖形性質,等邊三角形的性質,銳角三角函數定義,熟練掌握反比例函數的圖象與性質是解本題的關鍵.

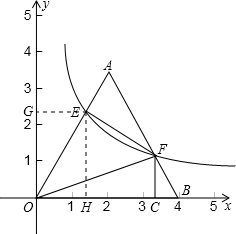
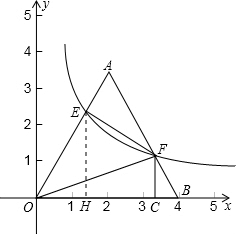
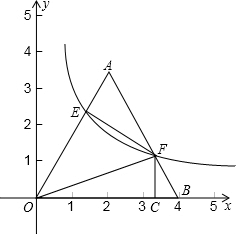 如圖,將邊長為4的等邊三角形AOB放置于平面直角坐標系xoy中,F是AB邊上的動點(不與端點A、B重合),過點F的反比例函數y=
如圖,將邊長為4的等邊三角形AOB放置于平面直角坐標系xoy中,F是AB邊上的動點(不與端點A、B重合),過點F的反比例函數y= (k>0,x>0)與OA邊交于點E,過點F作FC⊥x軸于點C,連結EF、OF.
(k>0,x>0)與OA邊交于點E,過點F作FC⊥x軸于點C,連結EF、OF. ,求反比例函數的解析式;
,求反比例函數的解析式; xy=
xy= ,
, ,
, ,
,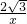 (x>0);
(x>0);
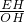 =
= ,
, m,OE=2m,
m,OE=2m, m),
m),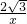 圖象上,
圖象上, m=
m=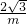 ,
, ,m2=-
,m2=- (舍去),
(舍去), ,EA=4-2
,EA=4-2 ,EG=
,EG= ,
, <
< ,
,
 x,FC=FB•sin∠FBC=
x,FC=FB•sin∠FBC= x,
x, x,
x, x,
x, x+2,
x+2, x+1,EH=OE•sin∠AOB=
x+1,EH=OE•sin∠AOB= x+
x+ ,
, x+1,
x+1, x+
x+ ),F(4-
),F(4- x,
x, x),
x), 的圖象上,
的圖象上, x+1)(
x+1)( x+
x+ )=(4-
)=(4- x)•
x)• x,
x, ,
,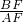 不存在,舍去;
不存在,舍去; 時,AF=
時,AF= ,BF:AF=1:4.
,BF:AF=1:4.

 數學奧賽暑假天天練南京大學出版社系列答案
數學奧賽暑假天天練南京大學出版社系列答案 南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案
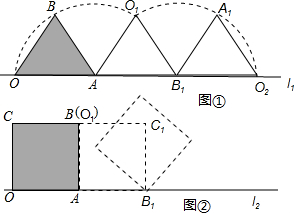
南大教輔搶先起跑暑假銜接教程南京大學出版社系列答案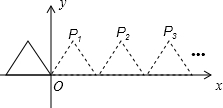 如圖,將邊長為2的等邊三角形沿x軸正方向連續翻折2012次,依次得到點P1,P2,P3…P2012.則點P2012的坐標是
如圖,將邊長為2的等邊三角形沿x軸正方向連續翻折2012次,依次得到點P1,P2,P3…P2012.則點P2012的坐標是