
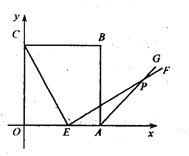
【題目】如圖,邊長為5的正方形 ![]() 的頂點
的頂點![]() 在坐標原點處,點
在坐標原點處,點![]() 分別在
分別在![]() 軸、
軸、![]() 軸的正半軸上,點
軸的正半軸上,點![]() 是
是![]() 邊上的點(不與點
邊上的點(不與點![]() 重合)
重合)![]() ,且與正方形外角平分線
,且與正方形外角平分線![]() 交于點
交于點![]() .
.
(1)求證:![]() ;
;
(2)若點![]() 坐標為
坐標為![]() 時,①在
時,①在![]() 軸上是否存在點
軸上是否存在點![]() ,使得四邊形
,使得四邊形![]() 是平行四邊形?若存在,求出點
是平行四邊形?若存在,求出點![]() 的坐標;若不存在,說明理由;
的坐標;若不存在,說明理由;
②在平面內是否存在點![]() ,使四邊形
,使四邊形![]() 為正方形,若存在,請直接寫出
為正方形,若存在,請直接寫出![]() 點坐標,若不存在,說明理由.
點坐標,若不存在,說明理由.
【答案】(1)見解析;(2)①存在,![]() ,理由見解析;②存在,
,理由見解析;②存在,![]() ,理由見解析
,理由見解析
【解析】
(1)在![]() 上截取
上截取![]() ,連結
,連結![]() ,利用正方形的性質,外角平分線和等量代換證明
,利用正方形的性質,外角平分線和等量代換證明![]() ,即可證明
,即可證明![]() ;
;
(2)過![]() 作
作![]() 交
交![]() 于
于![]() ,則點
,則點![]() 即為所求,利用平行四邊形和正方形的性質證明
即為所求,利用平行四邊形和正方形的性質證明![]() ,則有
,則有![]() ,進而可求出
,進而可求出![]() ,從而可確定M的坐標;
,從而可確定M的坐標;
(3)過點C作EP的平行線,過點P作CE的平行線,兩平行線的交點即為所求Q點,過點Q作![]() 交CB與點K, 利用正方形的性質證明
交CB與點K, 利用正方形的性質證明![]() ,則有
,則有![]() 進而可求
進而可求![]() ,從而可確定Q的坐標.
,從而可確定Q的坐標.
(1)證明:在![]() 上截取
上截取![]() ,連結
,連結![]() ,
,
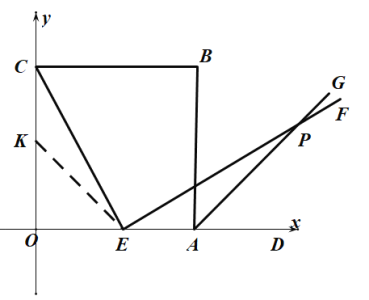
∵![]() 是正方形,
是正方形,
∴![]() ,
,
![]() ,
,
∴![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
∴![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
∵AG平分![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)①存在點![]() 使四邊形
使四邊形![]() 為平行四邊形,
為平行四邊形,
過![]() 作
作![]() 交
交![]() 于
于![]() ,則點
,則點![]() 即為所求,
即為所求,

∵![]() 是正方形,
是正方形,
∴![]() .
.
∵四邊形![]() 為平行四邊形,
為平行四邊形,
![]() .
.
∵![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴在![]() 軸上存在點
軸上存在點![]() ,使四邊形
,使四邊形![]() 的平行四邊形;
的平行四邊形;
②存在點Q使四邊形![]() 為正方形.
為正方形.
過點C作EP的平行線,過點P作CE的平行線,兩平行線的交點即為所求Q點,過點Q作![]() 交CB與點K,
交CB與點K,
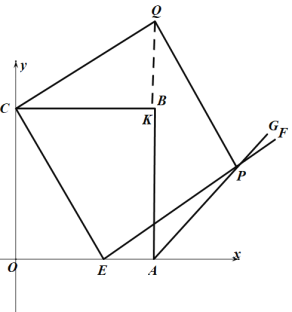
∵四邊形是正方形,
∴![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() (此時K與點B重合),
(此時K與點B重合),
![]() ,
,
![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,過點
,過點![]() 作直線
作直線![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉得到
順時針旋轉得到![]() (點
(點![]() 的對應點分別為
的對應點分別為![]() ).
).
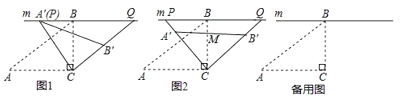
(1)問題發現如圖1,若![]() 與
與![]() 重合時,則
重合時,則![]() 的度數為____________;
的度數為____________;
(2)類比探究:如圖2,設![]() 與BC的交點為
與BC的交點為![]() ,當
,當![]() 為
為![]() 的中點時,求線段
的中點時,求線段![]() 的長;
的長;
(3)拓展延伸在旋轉過程中,當點![]() 分別在
分別在![]() 的延長線上時,試探究四邊形
的延長線上時,試探究四邊形![]() 的面積是否存在最小值.若存在,直接寫出四邊形
的面積是否存在最小值.若存在,直接寫出四邊形![]() 的最小面積;若不存在,請說明理由.
的最小面積;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商家在購進一款產品時,由于運輸成本及產品成本的提高,該產品第 x 天的成本 y(元/件)與 x(天)之間的關系如圖所示,并連續 60 天均以 80 元/件的價格出售, 第 x 天該產品的銷售量 z(件)與 x(天)滿足關系式 z=x+15.
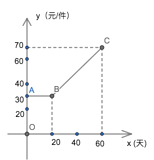
(1)第 25 天,該商家的成本是 元,獲得的利潤是 元;
(2)設第 x 天該商家出售該產品的利潤為 w 元.
①求 w 與 x 之間的函數關系式;
②求出第幾天的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某區教育局為了解今年九年級學生體育測試情況,隨機抽查了某班學生的體育測試成績為樣本,按A、B、C、D四個等級進行統計,并將統計結果繪制成如下的統計圖,請你結合圖中所給信息解答下列問題:


說明:A級:90分~100分;B級:75分~89分;C級:60分~74分;D級:60分以下
(1)樣本中D級的學生人數占全班學生人數的百分比是 ;
(2)扇形統計圖中A級所在的扇形的圓心角度數是 ;
(3)請把條形統計圖補充完整;
(4)若該校九年級有500名學生,請你用此樣本估計體育測試中A級和B級的學生人數之和.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是我國古代數學的經典著作,書中有一個問題:“今有黃金九枚,白銀一十一枚,稱之重適等.交易其一,金輕十三兩.問金、銀一枚各重幾何?”.意思是:甲袋中裝有黃金9枚(每枚黃金重量相同),乙袋中裝有白銀11枚(每枚白銀重量相同),稱重兩袋相等.兩袋互相交換1枚后,甲袋比乙袋輕了13兩(袋子重量忽略不計).問黃金、白銀每枚各重多少兩?設每枚黃金重x兩,每枚白銀重y兩,根據題意得( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下面的表格,根據表格解答下列問題:
| -2 | 0 | 1 |
| 1 | ||
| -3 | -3 |
(1)寫出![]() ,
,![]() ,
,![]() 的值;
的值;
(2)在直角坐標系中畫出二次函數![]() 的圖象;并根據圖象寫出使不等式
的圖象;并根據圖象寫出使不等式![]() 成立時
成立時![]() 的取值范圍;
的取值范圍;
(3)設該圖象與![]() 軸兩個交點分別為
軸兩個交點分別為![]() ,
,![]() ,與
,與![]() 軸交點為
軸交點為![]() ,直接寫出
,直接寫出![]() 的外心坐標.
的外心坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩地相距300千米,一輛貨車和一輛轎車先后從甲地出發駛向乙地如圖,如圖,線段OA表示貨車離甲地距離y(千米)與時間x(小時)之間的函數圖象;折線BCD表示轎車離甲地距離y(千米)與時間x(小時)之間的函數圖象;請根據圖象解答下到問題:
(1)貨車離甲地距離y(干米)與時間x(小時)之間的函數式為 ;
(2)當轎車與貨車相遇時,求此時x的值;
(3)在兩車行駛過程中,當轎車與貨車相距20千米時,求x的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個兩位數,用![]() 表示十位上的數,用
表示十位上的數,用![]() 表示個位上的數.
表示個位上的數.
(1)用含![]() ,
,![]() 的式子表示這個兩位數;
的式子表示這個兩位數;
(2)把這個兩位數個位上的數字與十位上的數字交換位置,得到一個新的兩位數.
①若原數個位上的數是十位上的數的3倍,且新數與原數的差是36,求原來的兩位數是多少?
②列式表示所得新數的平方與原數的平方的差(結果要化簡),并判斷其是11的倍數嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】電器專營店的經營利潤受地理位置、顧客消費能力等因素的影響,某品牌電腦專營店設有甲、乙兩家分店,均銷售A、B、C、D四種款式的電腦,每種款式電腦的利潤如表1所示.現從甲、乙兩店每月售出的電腦中各隨機抽取所記錄的50臺電腦的款式,統計各種款式電腦的銷售數量,如表2所示.
表1:四種款式電腦的利潤
電腦款式 | A | B | C | D |
利潤(元/臺) | 160 | 200 | 240 | 320 |
表2:甲、乙兩店電腦銷售情況
電腦款式 | A | B | C | D |
甲店銷售數量(臺) | 20 | 15 | 10 | 5 |
乙店銷售數量(臺)8 | 8 | 10 | 14 | 18 |
試運用統計與概率知識,解決下列問題:
(1)從甲店每月售出的電腦中隨機抽取一臺,其利潤不少于240元的概率為 ;
(2)經市場調查發現,甲、乙兩店每月電腦的總銷量相當.現由于資金限制,需對其中一家分店作出暫停營業的決定,若從每臺電腦的平均利潤的角度考慮,你認為應對哪家分店作出暫停營業的決定?并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com