
【題目】在菱形ABCD中,AC是對角線,CD=CE,連接DE,點M是線段DE的中點.
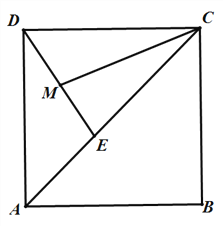
(1)如圖1,連接CM,若AC=16,CD=10,求DE的長
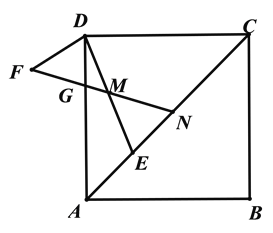
(2)如圖2,點F在菱形的外部,DF=DM,且∠CDA=∠FDE,連接FM交AD于點G,FM的延長線交AC于點N,求證:CN=AG.
【答案】(1)2![]() (2)證明見解析
(2)證明見解析
【解析】分析:(1)過D作DP⊥AC交AC于P,由菱形的性質,勾股定理求得DP,EP的長;(2)連接AF,CM,分別用SAS證明△AFD≌△CME,ASA證明△AFG≌△MNC.
詳解:(1)如圖,
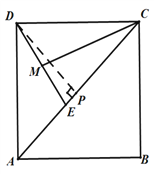
過D作DP⊥AC交AC于P,
∵DC=AD,DP⊥AC,∴CP=![]() AC=8.
AC=8.
又∵DC=10,∴DP=6.
∵EC=DC=10,∴AE=6.
∴EP=2,DE=![]() .
.
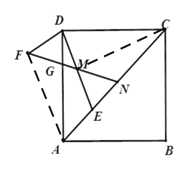
(2)連接AF,CM.
∵CD=CE,∴∠CDE=∠CED.
又∵∠CDA=∠FDE,∴∠FDA=∠CDE=∠CED.
在△AFD和△CME中
 ,
,
∴△AFD≌△CME.
∴∠FAD=∠MCE,AF=CM.
又∵FD=DM,∴∠DFM=∠DMF=∠EMN.
∵∠AFD=∠EMC,∠AFG+∠DFM=∠CMN+∠EMN
∴∠AFG=∠CMN
∴在△AFG和△MNC中
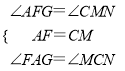 ,
,
∴△AFG≌△MNC,∴CN=AG.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】西安市某中學九年級組織了一次數學計算比賽(禁用計算器),每班選25名同學參加比賽,成績分為A,B,C,D四個等級,其中A等級得分為100分,B等級得分為85分,C等級得分為75分,D等級得分為60分,數學教研組將九年級一班和二班的成績整理并繪制成如下的統計圖,請根據提供的信息解答下列問題.
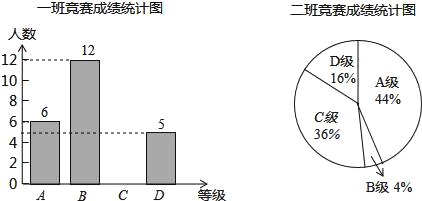
(1)把一班競賽成績統計圖補充完整.
(2)填表:
平均數(分) | 中位數(分) | 眾數(分) | |
一班 |
|
| 85 |
二班 | 84 | 75 |
|
(3)請從以下給出的兩個方面對這次比賽成績的結果進行①從平均數、眾數方面來比較一班和二班的成績;②從B級以上(包括B級)的人數方面來比較一班和二班的成績.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】泰興出租車司機小李某天下午的營運全是在東西走向的國慶路上進行的,若規定向東為正,向西為負,這天下午的行車里程如下(單位:千米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:千米).
(單位:千米).
(1)將最后一名乘客送到目的地后,小李距下午出發地點的距離是多少千米?
(2)若出租車每行駛![]() 耗油
耗油![]() ,這天下午這輛出租車共消耗多少升汽油?
,這天下午這輛出租車共消耗多少升汽油?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】任何一個正整數![]() 都可以寫成兩個正整數相乘的形式,我們把兩個乘數的差的絕對值最小的一種分解
都可以寫成兩個正整數相乘的形式,我們把兩個乘數的差的絕對值最小的一種分解![]() 稱為正整數
稱為正整數![]() 的最佳分解,并定義一個新運算
的最佳分解,并定義一個新運算![]() .例如:12=1×12=2×6=3×4,則
.例如:12=1×12=2×6=3×4,則![]() .那么以下結論中:①F(2)=
.那么以下結論中:①F(2)=![]() ;②F(24)=
;②F(24)=![]() ;③若
;③若![]() 是一個完全平方效,則
是一個完全平方效,則![]() ;④若
;④若![]() 是一個完全立方數(即
是一個完全立方數(即![]() ,
,![]() 是正整數),則
是正整數),則![]() .正確的個數為( )
.正確的個數為( )
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)用含有![]() 的式子表示判別式
的式子表示判別式![]() ________;
________;
(2)當![]() 在什么范圍內取值時,方程有兩個不相等的實數根;
在什么范圍內取值時,方程有兩個不相等的實數根;
(3)若該方程有兩個不相等的實數根![]() ,
,![]() ,問當
,問當![]() 取何值時
取何值時![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
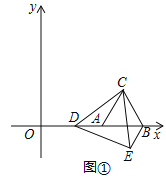
【題目】如圖①,在平面直角坐標系中,等邊△ABC的頂點A,B的坐標分別為(5,0),(9,0),點D是x軸正半軸上一個動點,連接CD,將△ACD繞點C逆時針旋轉60°得到△BCE,連接DE.
(Ⅰ)直接寫出點C的坐標,并判斷△CDE的形狀,說明理由;
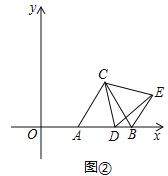
(Ⅱ)如圖②,當點D在線段AB上運動時,△BDE的周長是否存在最小值?若存在,求出△BDE的最小周長及此時點D的坐標;若不存在,說明理由;
(Ⅲ)當△BDE是直角三角形時,求點D的坐標.(直接寫出結果即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一列快車從甲地勻速駛往乙地,一列慢車從乙地勻速駛往甲地,設先發出車輛行駛的時間為 xh , 兩車之間的距離為ykm,圖中的折線表示 y與x之間的函數關系。根據圖象回答下列問題:
(1)慢車的速度為________ km/h,快車的速度為__________km/h;
(2)求線段CD所表示的y與x之間的函數關系式,并寫出自變量 x的取值范圍;
(3)當 x取何值時,兩車之間的距離為300 km?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的面積為12,△ABC是等邊三角形,點E在正方形ABCD內,對角線AC上有一點P使PE+PD的和最小,這個最小值為( )

A. ![]() B.
B. ![]() C. 3 D.
C. 3 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
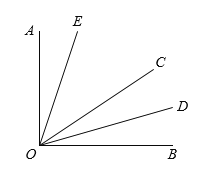
【題目】如圖,∠AOC與∠BOC互余,OD平分∠BOC,∠EOC=2∠AOE.
(1)若∠AOD=75°,求∠AOE的度數.
(2)若∠DOE=54°,求∠EOC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com