
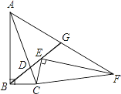
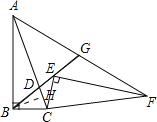
【題目】如圖,在Rt△ABC中,∠B=90°,sin∠BAC= ![]() ,點D是AC上一點,且BC=BD=2,將Rt△ABC繞點C旋轉到Rt△FEC的位置,并使點E在射線BD上,連接AF交射線BD于點G,則AG的長為________.
,點D是AC上一點,且BC=BD=2,將Rt△ABC繞點C旋轉到Rt△FEC的位置,并使點E在射線BD上,連接AF交射線BD于點G,則AG的長為________.
【答案】![]()
【解析】
根據旋轉的性質可得BC=CE,AC=CF,∠BCE=∠ACF,再根據等腰三角形兩底角相等求出∠CBD=∠CAF,從而得到△BCD和△AGD相似,根據相似三角形對應邊成比例求出AD=AG,過點B作BH⊥CD于H,根據等腰三角形三線合一的性質可得CD=2CH,再解直角三角形求出CH、AC的長,然后根據AD=AC-CD代入數據進行計算即可得解.
∵△ABC以點C為旋轉中心順時針旋轉得到△FEC,
∴BC=CE,AC=CF,∠BCE=∠ACF(為旋轉角),
∵∠CBD=![]() (180°-∠BCE),∠CAF=
(180°-∠BCE),∠CAF=![]() (180°-∠ACF),
(180°-∠ACF),
∴∠CBD=∠CAF,
又∵∠BDC=∠ADG,
∴△BCD∽△AGD,
∴![]() =
=![]() ,
,
∵BC=BD,
∴AG=AD,
則CD=2CH,
∵sin∠BAC=![]() ,BC=2,
,BC=2,
∴![]() =
=![]() =
=![]() ,
,
即![]() =
=![]() =
=![]() ,
,
解得CH=![]() ,AC=6,
,AC=6,
∴CD=2×![]() =
=![]() ,
,
AD=AC-CD=6-![]() =
=![]() ,
,
∴AG=AD=![]() .
.
故答案為:![]()


科目:初中數學 來源: 題型:
【題目】某社區準備在甲、乙兩位射箭愛好者中選出一人參加集訓,兩人各射了![]() 箭,他們的總成績(單位:環)相同.小宇根據他們的成績繪制了如圖尚不完整的統計圖表,并計算了甲成績的平均數和方差(見小宇的作業).
箭,他們的總成績(單位:環)相同.小宇根據他們的成績繪制了如圖尚不完整的統計圖表,并計算了甲成績的平均數和方差(見小宇的作業).
第 | 第 | 第 | 第 | 第 | |
甲成績 |
|
|
|
|
|
乙成績 |
|
|
|
|
|
(1)a=_________
(2)![]()
(3)參照小宇的計算方法,計算乙成績的方差;
(4)請你從平均數和方差的角度分析,誰將被選中.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() ,
,![]() 是關于
是關于![]() 的方程
的方程![]() 的兩實根,實數
的兩實根,實數![]() 、
、![]() 、
、![]() 、
、![]() 的大小關系可能是( )
的大小關系可能是( )
A. α<a<b<β B. a<α<β<b C. a<α<b<β D. α<a<β<b
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙倆射擊運動員進行10次射擊,甲的成績是7,7,8,9,8,9,10,9,9,9,乙的成績如圖所示.則甲、乙射擊成績的方差之間關系是![]()
![]() (填“<”,“=”,“>”).
(填“<”,“=”,“>”).
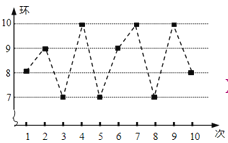
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某中學在創建“特色校園”的活動中,將本校的辦學理念做成宣傳牌AB,放置在教學樓的頂部(如圖所示)。小明在操場上的點D處,用1m高的測角儀CD,從點C測得宣傳牌的底部B的仰角為37,然后向教學樓正方向走了4米到達點F處,又從點E測得宣傳牌頂部A仰角為45.已知教學樓高BM=17米,且點A、B、M在同一直線上,求宣傳牌AB高度(結果精確到0.1米。參考數據:![]() ,sin37≈0.60,cos37≈0.81,tan37≈0.75).
,sin37≈0.60,cos37≈0.81,tan37≈0.75).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】先閱讀下列兩段材料,再解答下列問題:
(一)例題:分解因式:![]()
解:將“![]() ”看成整體,設
”看成整體,設![]() ,則原式
,則原式![]() ,
,
再將“![]() ”換原,得原式
”換原,得原式![]() ;
;
上述解題目用到的是:整體思想,“整體思想”是數學解題中常用的一種思想方法;
(二)常用因式分解的方法有提公因式法和公式法,但有的多項式只用上述一種方法無法分解,例如![]() ,我們細心觀察就會發現,前面兩項可以分解,后兩項也可以分解,分別分解后會產生公因式就可以完整分解了.
,我們細心觀察就會發現,前面兩項可以分解,后兩項也可以分解,分別分解后會產生公因式就可以完整分解了.
過程:![]()
![]() ,
,
這種方法叫分組分解法,對于超過三項的多項式往往考慮這種方法.
利用上述數學思想方法解決下列問題:
(1)分解因式:![]()
(2)分解因式:![]()
(3)分解因式:![]() ;
;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com