
 ,MN=2
,MN=2 .
. 是劣弧),且EF=5,把△OBC經過平移、旋轉和相似變換后,使它的兩個頂點分別與點E,F重合.在EF的同一側,這樣的三角形共有多少個?你能在其中找出另一個頂點在⊙O上的三角形嗎?請在圖中畫出這個三角形,并求出這個三角形與△OBC的周長之比.
是劣弧),且EF=5,把△OBC經過平移、旋轉和相似變換后,使它的兩個頂點分別與點E,F重合.在EF的同一側,這樣的三角形共有多少個?你能在其中找出另一個頂點在⊙O上的三角形嗎?請在圖中畫出這個三角形,并求出這個三角形與△OBC的周長之比.
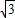 ,∠A=30°,
,∠A=30°,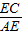 ,即EC=AEtan30°=3,
,即EC=AEtan30°=3,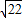 ,
, MN=
MN=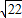 ,
, ,
,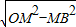 =
=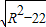 ,
,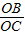 =
=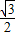 ,
,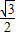 OC,
OC,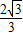 OB=
OB=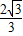
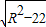 ,
,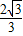
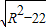 +3,
+3,
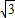 ,
,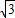 =15+5
=15+5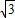 ,
,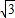 ,
,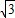 ):(3+
):(3+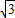 )=5:1.
)=5:1.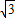 ,
,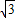 =15+5
=15+5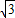 ,
,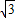 ):(3+
):(3+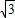 )=5:1.
)=5:1.

科目:初中數學 來源: 題型:
| 3 |
 ,MN=2
,MN=2| 22 |
 |
| FME |
查看答案和解析>>
科目:初中數學 來源:三點一測叢書 九年級數學 上 (江蘇版課標本) 江蘇版課標本 題型:013
如圖,AE切⊙O于點E,AC=CD=DB=10,則線段AE的長為

A.![]()
B.15
C.![]()
D.20
查看答案和解析>>
科目:初中數學 來源:2012年浙江省杭州市中考數學試卷 題型:044
如圖,AE切⊙O于點E,AT交⊙O于點M,N,線段OE交AT于點C,OB⊥AT于點B,已知∠EAT=30°,AE=3![]() ,MN=2
,MN=2![]() .
.

(1)求∠COB的度數;
(2)求⊙O的半徑R;
(3)點F在⊙O上(![]() 是劣弧),且EF=5,把△OBC經過平移、旋轉和相似變換后,使它的兩個頂點分別與點E,F重合.在EF的同一側,這樣的三角形共有多少個?你能在其中找出另一個頂點在⊙O上的三角形嗎?請在圖中畫出這個三角形,并求出這個三角形與△OBC的周長之比.
是劣弧),且EF=5,把△OBC經過平移、旋轉和相似變換后,使它的兩個頂點分別與點E,F重合.在EF的同一側,這樣的三角形共有多少個?你能在其中找出另一個頂點在⊙O上的三角形嗎?請在圖中畫出這個三角形,并求出這個三角形與△OBC的周長之比.
查看答案和解析>>
科目:初中數學 來源:浙江省中考真題 題型:解答題
 ,MN=2
,MN=2 .
. 是劣弧),且EF=5,把△OBC經過平移、旋轉和相似變換后,使它的兩個頂點分別與點E,F重合.在EF的同一側,這樣的三角形共有多少個?你能在其中找出另一個頂點在⊙O上的三角形嗎?請在圖中畫出這個三角形,并求出這個三角形與△OBC的周長之比.
是劣弧),且EF=5,把△OBC經過平移、旋轉和相似變換后,使它的兩個頂點分別與點E,F重合.在EF的同一側,這樣的三角形共有多少個?你能在其中找出另一個頂點在⊙O上的三角形嗎?請在圖中畫出這個三角形,并求出這個三角形與△OBC的周長之比.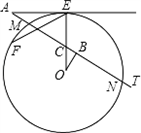
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com