
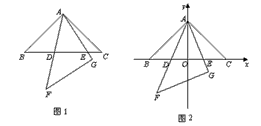
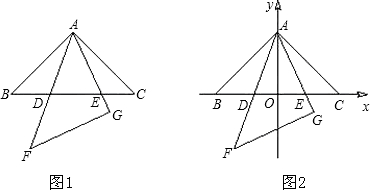
| 解:(1)△ABE∽△DAE, △ABE∽△DCA。 ∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°, ∴∠BAE=∠CDA, 又∠B=∠C=45°, ∴△ABE∽△DCA。 (2)∵△ABE∽△DCA, ∴ 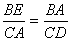 , ,由依題意可知,CA=BA= 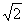 , , ∴ 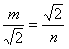 , ,∴m=  , ,∴自變量n的取值范圍為1<n<2。 (3)由BD=CE,可得BE=CD,即m=n, ∵m= 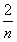 , ,∴m=n= 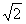 , ,∵OB=OC=  BC=1, BC=1,∴OE=OD=  -1, -1,∴D(1-  , 0), , 0),∴BD=OB-OD=1-(  -1)=2- -1)=2-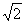 =CE, DE=BC-2BD=2-2(2- =CE, DE=BC-2BD=2-2(2- )=2 )=2 -2, -2,∵BD2+CE2=(2BD)2=4(2- 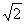 )2=12-8 )2=12-8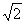 , DE=(2-2 , DE=(2-2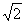 )2= 12-8 )2= 12-8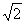 , ,∴BD2+CE2=DE2。 |
|
| (4)成立。 證明:如圖,將△ACE繞點A順時針旋轉90°至△ABH的位置, 則CE=HB,AE=AH, ∠ABH=∠C=45°,旋轉角∠EAH=90°, 連接HD, 在△EAD和△HAD中, ∵AE=AH,∠HAD=∠EAH-∠FAG=45°=∠EAD,AD=AD, ∴△EAD≌△HAD, ∴DH=DE, 又∠HBD=∠ABH+∠ABD=90°, ∴BD2+HB2=DH2, 即BD2+CE2=DE2。 |
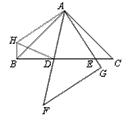 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
| 3 |
| 3 |
| 3 |
| 2 |

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com