
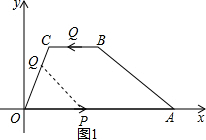
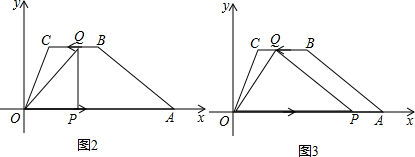
 (2013•黃岡)如圖,在平面直角坐標系中,四邊形ABCD是梯形,其中A(6,0),B(3,
(2013•黃岡)如圖,在平面直角坐標系中,四邊形ABCD是梯形,其中A(6,0),B(3,| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
|
|
| ||
| 15 |
4
| ||
| 15 |
4
| ||
| 5 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3+(3-t)2 |
| 3+[2t-(3-t)]2 |
| 3+(3t-3)2 |
| ||
| 15 |
4
| ||
| 15 |
4
| ||
| 5 |
| ||
| 15 |
16
| ||
| 15 |
| ||
| 3 |
2
| ||
| 3 |
|
|
| ||
| 3(1-t) |
2
| ||
| 3(1-t) |
| 3 |
| 3 |
| 3 |
| 3 |
| 4-t |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 3 |
| 4-t |
| 2 |
| 4 |
| 3 |


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源: 題型:
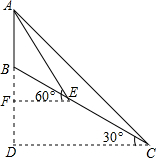 (2013•黃岡)如圖,小山頂上有一信號塔AB,山坡BC的傾角為30°,現為了測量塔高AB,測量人員選擇山腳C處為一測量點,測得塔頂仰角為45°,然后順山坡向上行走100米到達E處,再測得塔頂仰角為60°,求塔高AB(結果保留整數,
(2013•黃岡)如圖,小山頂上有一信號塔AB,山坡BC的傾角為30°,現為了測量塔高AB,測量人員選擇山腳C處為一測量點,測得塔頂仰角為45°,然后順山坡向上行走100米到達E處,再測得塔頂仰角為60°,求塔高AB(結果保留整數,| 3 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com