
 如圖,已知對稱軸為x=-
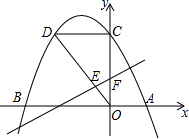
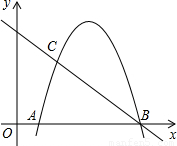
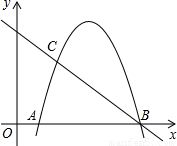
如圖,已知對稱軸為x=- 的拋物線y=ax2+bx+6與x軸交于A、B兩點,與y軸交于C點,OA=3,D是拋物線上一點,且DC⊥OC.
的拋物線y=ax2+bx+6與x軸交于A、B兩點,與y軸交于C點,OA=3,D是拋物線上一點,且DC⊥OC. x+m與OD交于點E,與y軸交于點F,若OE:DE=1:2,求m的值;
x+m與OD交于點E,與y軸交于點F,若OE:DE=1:2,求m的值; ,經(jīng)過點A(3,0),
,經(jīng)過點A(3,0),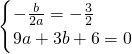 ,解得
,解得 ,
, ∴拋物線解析式為y=-
∴拋物線解析式為y=- x2-x+6;
x2-x+6; x2-x+6,
x2-x+6, x2-x+6=6,
x2-x+6=6,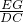 =
=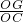 =
= =
= ,
, DC=1,OG=
DC=1,OG= OC=2,
OC=2, x+m,
x+m, +m,
+m, ;
;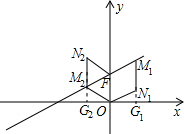 (3)若M是直線EF上一動點,在x軸上方存在點N,使以O(shè)、F、M、N為頂點的四邊形是菱形.
(3)若M是直線EF上一動點,在x軸上方存在點N,使以O(shè)、F、M、N為頂點的四邊形是菱形. ,
, x+
x+ 上,
上, a+
a+ )(a>0),則點N1的坐標(biāo)為(a,
)(a>0),則點N1的坐標(biāo)為(a, a),
a), a)2=(
a)2=( )2,
)2, ,
, ,
, );
); )(a>0),則點N2的坐標(biāo)為(-2,4);
)(a>0),則點N2的坐標(biāo)為(-2,4);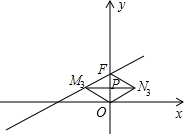 ②如圖,OF為菱形的對角線時,連接M3N3,交OF于點P,則M3N3與OF互相垂直平分,
②如圖,OF為菱形的對角線時,連接M3N3,交OF于點P,則M3N3與OF互相垂直平分, OF=
OF= ,
, 時,
時, x+
x+ =
= ,
, ,
, ,
, ),
), ,
, ).
). ,
, ),N2(-2,4),N3(
),N2(-2,4),N3( ,
, ).
). x2-x+6與y軸交點C的坐標(biāo)為(0,6),將y=6代入,求出x的值,得到D點坐標(biāo)及DC=3,再過點E作EG⊥y軸于點G,由EG∥DC,得到△OEG∽△ODC,根據(jù)相似三角形對應(yīng)邊成比例得出
x2-x+6與y軸交點C的坐標(biāo)為(0,6),將y=6代入,求出x的值,得到D點坐標(biāo)及DC=3,再過點E作EG⊥y軸于點G,由EG∥DC,得到△OEG∽△ODC,根據(jù)相似三角形對應(yīng)邊成比例得出 =
=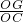 =
=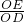 =
= ,求出EG,OG的值,得出E點坐標(biāo),然后將E點坐標(biāo)代入y=
,求出EG,OG的值,得出E點坐標(biāo),然后將E點坐標(biāo)代入y= x+m,即可求出m的值;
x+m,即可求出m的值; a+
a+ ),則點N1的坐標(biāo)為(a,
),則點N1的坐標(biāo)為(a, a),在Rt△OG1N1中,運用勾股定理得出OG12+G1N12=ON12,列出關(guān)于a的方程,解方程即可,同理求出點N2的坐標(biāo);②OF為菱形的對角線時,連接M3N3,交OF于點P,根據(jù)菱形的性質(zhì)可知M3N3與OF互相垂直平分,則OP=
a),在Rt△OG1N1中,運用勾股定理得出OG12+G1N12=ON12,列出關(guān)于a的方程,解方程即可,同理求出點N2的坐標(biāo);②OF為菱形的對角線時,連接M3N3,交OF于點P,根據(jù)菱形的性質(zhì)可知M3N3與OF互相垂直平分,則OP= OF=
OF= ,將y=
,將y= 代入y=
代入y= x+
x+ ,求出x的值,進(jìn)而得到點N3的坐標(biāo).
,求出x的值,進(jìn)而得到點N3的坐標(biāo).

 全優(yōu)考典單元檢測卷及歸類總復(fù)習(xí)系列答案
全優(yōu)考典單元檢測卷及歸類總復(fù)習(xí)系列答案科目:初中數(shù)學(xué) 來源: 題型:
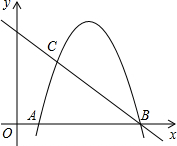 M、N、B為頂點的三角形與△ABC相似,寫出計算過程.
M、N、B為頂點的三角形與△ABC相似,寫出計算過程.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
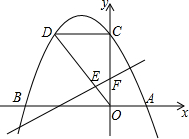 如圖,已知對稱軸為x=-
如圖,已知對稱軸為x=-| 3 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2012年湖北省黃岡市浠水縣華桂中學(xué)中考數(shù)學(xué)模擬試卷(解析版) 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源:2011年湖北省黃岡中學(xué)啟黃初中中考數(shù)學(xué)二模試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com