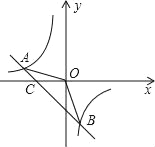
【題目】如圖，一次函數y=kx+b的圖象與反比例函數y=
的圖象交于A（﹣2，1），B（1，n）．
（1）試確定上述反比例函數和一次函數的表達式；
（2）求△ABO的面積；
（3）根據圖象寫出使反比例函數的值大于一次函數值的自變量x的取值范圍．
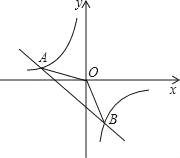
【答案】（1）y=-
，y=-x-1（2）1.5（3）﹣2＜x＜0或x＞1
【解析】試題分析：(1)待定系數法求函數表達式.(2)三角形面積公式求解.(3)根據圖象的高低求出范圍.
試題解析：
（1）∵把A（﹣2，1）代入y=
得：m=﹣2，
∴反比例函數的解析式是y=﹣
．
∵把B（1，n）代入反比例函數y=﹣
得：n=﹣2，
∴B的坐標是（1，﹣2），
把A、B的坐標代入一次函數y=kx+b得： 
，
解得：k=﹣1，b=﹣1，
∴一次函數的解析式是y=﹣x﹣1；
（2）設一次函數與x軸交于點C．
把y=0代入y=﹣x﹣1，得：0=﹣x﹣1，交點x=﹣1，
∴C（﹣1，0），
∴△AOB的面積=SAOC+S△BOC=
×|﹣1|×1+
×|﹣1|×|﹣2|=1.5；
（3）從圖象可知：當反比例函數的值大于一次函數值時x的取值范圍﹣2＜x＜0或x＞1．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】在一條直路上的
、
、
、
四個車站的位置如圖所示（單位千米），如果小明家在站旁，他的同學小亮家在站旁，新華書店在站旁，一天小明乘車從站出發到站下車去新華書店購買一些課外閱讀書籍，途徑、兩站，當小明到達站時發現自己所帶錢不夠購買自己所要的書籍.于是他乘車返回到站處下車向小亮借足了錢，然后乘車繼續趕往站旁的新華書店.
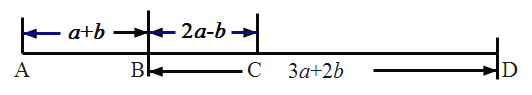
（1）求、兩站的距離；（用含有
、
的代數式表示）
（2）求這一天小明從站到站乘車路程.（用含有、的代數式表示）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小強打算找印刷公司設計一款新年賀卡并印刷.如圖1是甲印刷公司設計與印刷卡片計價方式的說明（包含設計費與印刷費），乙公司的收費與印刷卡片數量的關系如圖2所示.
（1）分別寫出甲乙兩公司的收費y（元）與印刷數量x之間的關系式.
（2）如果你是小強，你會選擇哪家公司？并說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，平行四邊形ABCD中，E，F分別為AD，BC邊上的一點，增加下列條件，不能得出BE∥DF的是（ ）
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，拋物線
（a≠0）的圖象與x軸交于A、B兩點，與y軸交于C點，已知B點坐標為（4，0）．
（1）求拋物線的解析式；
（2）試探究△ABC的外接圓的圓心位置，并求出圓心坐標；
（3）若點M是線段BC下方的拋物線上一點，求△MBC的面積的最大值，并求出此時M點的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△BAC中，∠BAC=90°，將△ABC繞點A順時針旋轉90°得到△AB′C′（點B的對應點是點B′，點C的對應點是點C′），連接CC′，若∠CC′B′=30°，求∠B的度數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y=﹣
x+
分別與x軸、y軸交于B，C兩點，點A在x軸上，∠ACB=90°，拋物線y=ax2+bx+
經過A，B兩點，A點坐標為（﹣1，0）．
（1）求B、C兩點的坐標；
（2）求拋物線的解析式；
（3）點M是直線BC上方拋物線上的一點，過點M作MH⊥BC于點H，作MD∥y軸交BC于點D，求△DMH周長的最大值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：正方形ABCD，E為平面內任意一點，連接DE，將線段DE繞點D順時針旋轉90°得到DG，連接EC，AG．
（1）當點E在正方形ABCD內部時，
①根據題意，在圖1中補全圖形；
②判斷AG與CE的數量關系與位置關系并寫出證明思路．
（2）當點B，D，G在一條直線時，若AD＝4，DG＝
，求CE的長．（可在備用圖中畫圖）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校八年級甲，乙兩班各有
名學生，為了解這兩個班學生身體素質情況，進行了抽樣調查.從這兩個班各隨機抽取
名學生進行身體素質測試，測試成績如下：
甲班
乙班
整理上面數據，得到如下統計表：
樣本數據的平均數、眾數.中位數如下表所示：
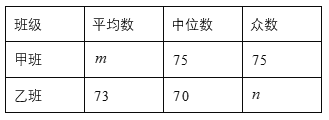
根據以上信息，解答下列問題：
（1）求表中
的值
（2）表中
的值為（ ）
（3）若規定測試成績在分以上（含分）的學生身體素質為優秀，請估計乙班名學生中身體素質為優秀的學生的人數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com