
以△ABC的三個頂點為圓心,以半徑為0.5cm作⊙A、⊙B、⊙C,且⊙A、⊙B、⊙C兩兩不相交,則⊙A、⊙B、⊙C被△ABC的三邊所截得的三個扇形的積和為
[ ]

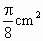
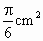
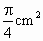
 互動英語系列答案
互動英語系列答案科目:初中數學 來源: 題型:閱讀理解
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
查看答案和解析>>
科目:初中數學 來源:2012年初中畢業升學考試(山東青島卷)數學(帶解析) 題型:解答題
問題提出:以n邊形的n個頂點和它內部的m個點,共(m+n)個點作為頂
點,可把原n邊形分割成多少個互不重疊的小三角形?
問題探究:為了解決上面的問題,我們將采取一般問題特殊化的策略,先從簡單和具體的情形入手:
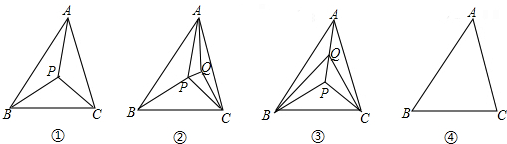
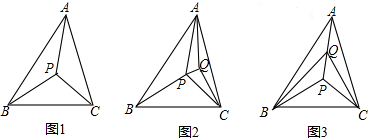
探究一:以△ABC的3個頂點和它內部的1個點P,共4個點為頂點,可把△ABC分割成多少個互
不重疊的小三角形?如圖①,顯然,此時可把△ABC分割成3個互不重疊的小三角形.
探究二:以△ABC的3個頂點和它內部的2個點P、Q,共5個點為頂點,可把△ABC分割成多少個
互不重疊的小三角形?
在探究一的基礎上,我們可看作在圖①△ABC的內部,再添加1個點Q,那么點Q的位置會有兩種
情況:
一種情況,點Q在圖①分割成的某個小三角形內部.不妨設點Q在△PAC的內部,如圖②;
另一種情況,點Q在圖①分割成的小三角形的某條公共邊上.不妨設點Q在PA上,如圖③.
顯然,不管哪種情況,都可把△ABC分割成5個互不重疊的小三角形.
探究三:以△ABC的三個頂點和它內部的3個點P、Q、R,共6個點為頂點,可把△ABC分割成 個
互不重疊的小三角形,并在圖④中畫出一種分割示意圖.
探究四:以△ABC的三個頂點和它內部的m個點,共(m+3)個點為頂點,可把△ABC分割成 個
互不重疊的小三角形.
探究拓展:以四邊形的4個頂點和它內部的m個點,共(m+4)個點為頂點,可把四邊形分割成
個互不重疊的小三角形.
問題解決:以n邊形的n個頂點和它內部的m個點,共(m+n)個點作為頂點,可把原n邊形分割成
個互不重疊的小三角形.
實際應用:以八邊形的8個頂點和它內部的2012個點,共2020個頂點,可把八邊形分割成多少個互
不重疊的小三角形?(要求列式計算)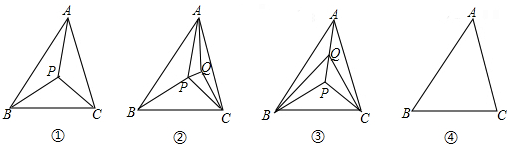
查看答案和解析>>
科目:初中數學 來源:2012年初中畢業升學考試(山東青島卷)數學(解析版) 題型:解答題
問題提出:以n邊形的n個頂點和它內部的m個點,共(m+n)個點作為頂
點,可把原n邊形分割成多少個互不重疊的小三角形?
問題探究:為了解決上面的問題,我們將采取一般問題特殊化的策略,先從簡單和具體的情形入手:
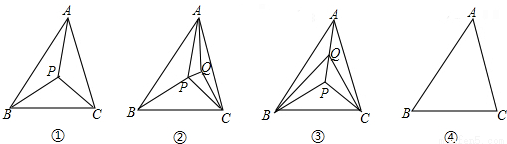
探究一:以△ABC的3個頂點和它內部的1個點P,共4個點為頂點,可把△ABC分割成多少個互
不重疊的小三角形?如圖①,顯然,此時可把△ABC分割成3個互不重疊的小三角形.
探究二:以△ABC的3個頂點和它內部的2個點P、Q,共5個點為頂點,可把△ABC分割成多少個
互不重疊的小三角形?
在探究一的基礎上,我們可看作在圖①△ABC的內部,再添加1個點Q,那么點Q的位置會有兩種
情況:
一種情況,點Q在圖①分割成的某個小三角形內部.不妨設點Q在△PAC的內部,如圖②;
另一種情況,點Q在圖①分割成的小三角形的某條公共邊上.不妨設點Q在PA上,如圖③.
顯然,不管哪種情況,都可把△ABC分割成5個互不重疊的小三角形.
探究三:以△ABC的三個頂點和它內部的3個點P、Q、R,共6個點為頂點,可把△ABC分割成 個
互不重疊的小三角形,并在圖④中畫出一種分割示意圖.
探究四:以△ABC的三個頂點和它內部的m個點,共(m+3)個點為頂點,可把△ABC分割成 個
互不重疊的小三角形.
探究拓展:以四邊形的4個頂點和它內部的m個點,共(m+4)個點為頂點,可把四邊形分割成
個互不重疊的小三角形.
問題解決:以n邊形的n個頂點和它內部的m個點,共(m+n)個點作為頂點,可把原n邊形分割成
個互不重疊的小三角形.
實際應用:以八邊形的8個頂點和它內部的2012個點,共2020個頂點,可把八邊形分割成多少個互
不重疊的小三角形?(要求列式計算)

查看答案和解析>>
科目:初中數學 來源:2012年山東省青島市中考數學試卷(解析版) 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com