
【題目】如圖1,在Rt△ABC中,∠ACB=90°,點D是邊AB的中點,點E在邊BC上,AE=BE,點M是AE的中點,聯結CM,點G在線段CM上,作∠GDN=∠AEB交邊BC于N. 
(1)如圖2,當點G和點M重合時,求證:四邊形DMEN是菱形;
(2)如圖1,當點G和點M、C不重合時,求證:DG=DN.
【答案】
(1)證明:如圖2中,

∵AM=ME.AD=DB,
∴DM∥BE,
∴∠GDN+∠DNE=180°,
∵∠GDN=∠AEB,
∴∠AEB+∠DNE=180°,
∴AE∥DN,
∴四邊形DMEN是平行四邊形,
∵DM= ![]() BE,EM=
BE,EM= ![]() AE,AE=BE,
AE,AE=BE,
∴DM=EM,
∴四邊形DMEN是菱形
(2)如圖1中,取BE的中點F,連接DM、DF.

由(1)可知四邊形EMDF是菱形,
∴∠AEB=∠MDF,DM=DF,
∴∠GDN=∠AEB,
∴∠MDF=∠GDN,
∴∠MDG=∠FDN,
∵∠DFN=∠AEB=∠MCE,∠GMD=∠EMD+∠CME,、
在Rt△ACE中,∵AM=ME,
∴CM=ME,
∴∠MCE=∠CEM=∠EMD,
∴∠DMG=∠DFN,
∴△DMG≌△DFN,
∴DG=DN.
【解析】(1)如圖2中,首先證明四邊形DMEN是平行四邊形,再證明ME=MD即可證明.(2)如圖1中,取BE的中點F,連接DM、DF.只要證明△DMG≌△DFN即可.


科目:初中數學 來源: 題型:
【題目】如圖所示,在平行四邊形ABCD中,AE平分∠BAD,交BC于點E,BF平分∠ABC,交AD于點F,AE與BF交于點P,連接EF,PD. 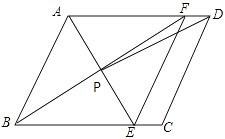
(1)求證:四邊形ABEF是菱形.
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,設反比例函數的解析式為y= ![]() (k>0).
(k>0). 
(1)若該反比例函數與正比例函數y=2x的圖象有一個交點的縱坐標為2,求k的值;
(2)若該反比例函數與過點M(﹣2,0)的直線l:y=kx+b的圖象交于A,B兩點,如圖所示,當△ABO的面積為 ![]() 時,求直線l的解析式.
時,求直線l的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市東坡實驗中學準備開展“陽光體育活動”,決定開設足球、籃球、乒乓球、羽毛球、排球等球類活動,為了了解學生對這五項活動的喜愛情況,隨機調查了m名學生(每名學生必選且只能選擇這五項活動中的一種).
根據以上統計圖提供的信息,請解答下列問題:
(1)m= , n= .
(2)補全上圖中的條形統計圖.
(3)若全校共有2000名學生,請求出該校約有多少名學生喜愛打乒乓球.
(4)在抽查的m名學生中,有小薇、小燕、小紅、小梅等10名學生喜歡羽毛球活動,學校打算從小薇、小燕、小紅、小梅這4名女生中,選取2名參加全市中學生女子羽毛球比賽,請用列表法或畫樹狀圖法,求同時選中小紅、小燕的概率.(解答過程中,可將小薇、小燕、小紅、小梅分別用字母A、B、C、D代表)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,點D、E分別是邊AB、AC的中點,延長DE到F,使得EF=DE,那么四邊形ADCF是( ) 
A.等腰梯形
B.直角梯形
C.矩形
D.菱形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明用棋子擺放圖形來研究數的規律.圖1中棋子圍成三角形,其棵數3,6,9,12,…稱為三角形數.類似地,圖2中的4,8,12,16,…稱為正方形數.下列數中既是三角形數又是正方形數的是( )
A.2010
B.2012
C.2014
D.2016
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1所示,E為矩形ABCD的邊AD上一點,動點P、Q同時從點B出發,點P以1cm/秒的速度沿折線BE﹣ED﹣DC運動到點C時停止,點Q以2cm/秒的速度沿BC運動到點C時停止.設P、Q同時出發t秒時,△BPQ的面積為ycm2 . 已知y與t的函數關系圖象如圖2;(其中曲線OG為拋物線的一部分,其余各部分均為線段),則下列結論:
①當0<t≤5時,y= ![]() t2;②當t=6秒時,△ABE≌△PQB;③cos∠CBE=
t2;②當t=6秒時,△ABE≌△PQB;③cos∠CBE= ![]() ;④當t=
;④當t= ![]() 秒時,△ABE∽△QBP;
秒時,△ABE∽△QBP;
其中正確的是( )
A.①②
B.①③④
C.③④
D.①②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在平面直角坐標系xOy中,直線y= ![]() x+6與x軸、y軸的交點分別為A、B兩點,將∠OBA對折,使點O的對應點H落在直線AB上,折痕交x軸于點C.
x+6與x軸、y軸的交點分別為A、B兩點,將∠OBA對折,使點O的對應點H落在直線AB上,折痕交x軸于點C.
(1)直接寫出點C的坐標,并求過A、B、C三點的拋物線的解析式;
(2)若(1)中拋物線的頂點為D,在直線BC上是否存在點P,使得四邊形ODAP為平行四邊形?若存在,求出點P的坐標;若不存在,說明理由;
(3)若把(1)中的拋物線向左平移3.5個單位,則圖象與x軸交于F、N(點F在點N的左側)兩點,交y軸于E點,則在此拋物線的對稱軸上是否存在一點Q,使點Q到E、N兩點的距離之差最大?若存在,請求出點Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,過C點的切線CE垂直于弦AD于點E,連OD交AC于點F. 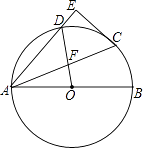
(1)求證:∠BAC=∠DAC;
(2)若AF:FC=6:5,求sin∠BAC的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com