
【題目】如圖,在△ABC中,∠BAC=90°,AB=AC=6,D為BC的中點. 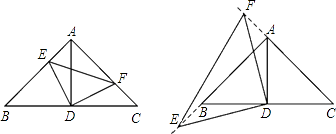
(1)若E、F分別是AB、AC上的點,且AE=CF,求證:△AED≌△CFD;
(2)當點F、E分別從C、A兩點同時出發,以每秒1個單位長度的速度沿CA、AB運動,到點A、B時停止;設△DEF的面積為y,F點運動的時間為x,求y與x的函數關系式;
(3)在(2)的條件下,點F、E分別沿CA、AB的延長線繼續運動,求此時y與x的函數關系式.
【答案】
(1)證明:∵∠BAC=90° AB=AC=6,D為BC中點
∴∠BAD=∠DAC=∠B=∠C=45°
∴AD=BD=DC
∵AE=CF∴△AED≌△CFD(SAS)
(2)解:依題意有:FC=AE=x,
∵△AED≌△CFD
∴S四邊形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=9
∴ ![]() S四邊形AEDF-
S四邊形AEDF- ![]()
∴ ![]() ;
;
(3)解:依題意有:AF=BE=x﹣6,AD=DB,∠ABD=∠DAC=45°
∴∠DAF=∠DBE=135°
∴△ADF≌△BDE
∴S△ADF=S△BDE
∴S△EDF=S△EAF+S△ADB
= ![]()
∴ ![]() .
.

【解析】(1)利用等腰直角三角形的性質得到∠BAD=∠DAC=∠B=∠C=45°,進而得到AD=BD=DC,為證明△AED≌△CFD提供了重要的條件;(2)利用S四邊形AEDF=S△AED+S△ADF=S△CFD+S△ADF=S△ADC=9 即可得到y與x之間的函數關系式;(3)依題意有:AF=BE=x﹣6,AD=DB,∠ABD=∠DAC=45°得到∠DAF=∠DBE=135°,從而得到△ADF≌△BDE,利用全等三角形面積相等得到S△ADF=S△BDE從而得到S△EDF=S△EAF+S△ADB即可確定兩個變量之間的函數關系式.
【考點精析】關于本題考查的等腰直角三角形,需要了解等腰直角三角形是兩條直角邊相等的直角三角形;等腰直角三角形的兩個底角相等且等于45°才能得出正確答案.


科目:初中數學 來源: 題型:
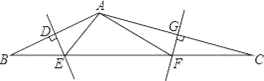
【題目】如圖,在△ABC中,AB、AC的垂直平分線分別交BC于點E、F.
(1)若△AEF的周長為10cm,則BC的長為______cm.
(2)若∠EAF=100°,則∠BAC______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】手機上網已經成為當今年輕人時尚的網絡生活,某網絡公司看中了這種商機,推出了兩種手機上網的計費方式:方式A以每分鐘0.1元的價格按上網時間計費;方式B除收月基費20元外,再以每分鐘0.06元的價格按上網時間計費.假設某客戶月手機上網的時間為x分鐘,上網費用為y元. 
(1)分別寫出該客戶按A、B兩種方式的上網費y(元)與每月上網時間x(分鐘)的函數關系式,并在右圖的坐標系中畫出這兩個函數的圖象;
(2)如何選擇計費方式能使該客戶上網費用更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市正在進行商業街改造,商業街起點在古民居P的南偏西60°方向上的A處,現已改造至古民居P南偏西30°方向上的B處,A與B相距150m,且B在A的正東方向.為不破壞古民居的風貌,按照有關規定,在古民居周圍100m以內不得修建現代化商業街.若工程隊繼續向正東方向修建200m商業街到C處,則對于從B到C的商業街改造是否違反有關規定?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩輛摩托車同時從相距20km的A,B兩地出發,相向而行.圖中l1,l2分別表示甲、乙兩輛摩托車到A地的距離s(km)與行駛時間t(h)的函數關系.則下列說法錯誤的是
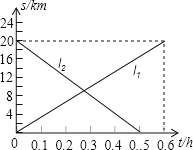
A. 乙摩托車的速度較快
B. 經過0.3小時甲摩托車行駛到A,B兩地的中點
C. 經過0.25小時兩摩托車相遇
D. 當乙摩托車到達A地時,甲摩托車距離A地![]() km
km
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用火柴棒按下圖的方式搭塔式三角形,第一個圖用了3根火柴棒,第二個圖用了9根火柴棒,第三個圖用了18根火柴棒,......,照這樣下去,第9個圖用了_____根火柴棒.
 ……
……
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】作圖與計算
(1)已知:![]() .
.
求作:在圖2中,以OA為一邊,在∠AOB的內部作.∠AOC=![]() (要求:直尺和圓規作圖,不寫作法,保留圖痕跡.)
(要求:直尺和圓規作圖,不寫作法,保留圖痕跡.)

(2)過點O分別引射線OA、OB、OC,且∠AOB=65°,∠BOC=30°,求∠AOC的度數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com