
【題目】如圖,線(xiàn)段![]() ,
,![]() 為
為![]() 的中點(diǎn),動(dòng)點(diǎn)
的中點(diǎn),動(dòng)點(diǎn)![]() 到點(diǎn)
到點(diǎn)![]() 的距離是1,連接
的距離是1,連接![]() ,線(xiàn)段
,線(xiàn)段![]() 繞點(diǎn)
繞點(diǎn)![]() 逆時(shí)針旋轉(zhuǎn)90°得到線(xiàn)段
逆時(shí)針旋轉(zhuǎn)90°得到線(xiàn)段![]() ,連接
,連接![]() ,則線(xiàn)段
,則線(xiàn)段![]() 長(zhǎng)度的最大值是( )
長(zhǎng)度的最大值是( )
A.2B.3C.![]() D.
D.![]()
【答案】D
【解析】
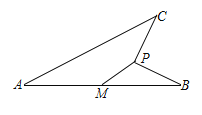
以M為坐標(biāo)原點(diǎn)建立坐標(biāo)系,過(guò)點(diǎn)C作CD⊥y軸,垂足為D,過(guò)點(diǎn)P作PE⊥DC,垂足為E,延長(zhǎng)EP交x軸于點(diǎn)F,設(shè)點(diǎn)P的坐標(biāo)為(x,y),則x2+y2=1.然后證明△ECP≌△FPB,由全等三角形的性質(zhì)得到EC=PF=y,FB=EP=2x,從而得到點(diǎn)C(x+y,y+2x),再由勾股定理可求得AC=![]() ,最后,依據(jù)當(dāng)y=1時(shí),AC有最大值求解即可.
,最后,依據(jù)當(dāng)y=1時(shí),AC有最大值求解即可.
解:如圖所示:以M為坐標(biāo)原點(diǎn)建立坐標(biāo)系,連接BC,過(guò)點(diǎn)C作CD⊥y軸,垂足為D,過(guò)點(diǎn)P作PE⊥DC,垂足為E,延長(zhǎng)EP交x軸于點(diǎn)F.

∵AB=4,M為AB的中點(diǎn),
∴A(2,0),B(2,0),
設(shè)點(diǎn)P的坐標(biāo)為(x,y),則x2+y2=1,
∵∠EPC+∠BPF=90°,∠EPC+∠ECP=90°,
∴∠ECP=∠FPB,
由旋轉(zhuǎn)的性質(zhì)可知:PC=PB,
在△ECP和△FPB中,
 ,
,
∴△ECP≌△FPB(AAS),
∴EC=PF=y,EP=FB=2x,
∴C(x+y,y+2x),
∴AC=![]() ,
,
∵x2+y2=1,
∴AC=![]() ,
,
∵1≤y≤1,
∴當(dāng)y=1時(shí),AC有最大值,AC的最大值為![]() ,
,
故答案為:![]() .
.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線(xiàn)![]() 的圖象經(jīng)過(guò)點(diǎn)A(2,-8),求:
的圖象經(jīng)過(guò)點(diǎn)A(2,-8),求:
(1)該拋物線(xiàn)的解析式;
(2)判斷點(diǎn)B(3,-18)是否在該拋物線(xiàn)上;
(3)求出此拋物線(xiàn)上縱坐標(biāo)是-50的點(diǎn)的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平而直角坐標(biāo)系中,一次函數(shù)y=﹣4x+4的圖象與x軸、y軸分別交于A、B兩點(diǎn).正方形ABCD的項(xiàng)點(diǎn)C、D在第一象限,頂點(diǎn)D在反比例函數(shù)y=![]() (k≠0)的圖象上.若正方形ABCD向左平移n個(gè)單位后,頂點(diǎn)C恰好落在反比例函數(shù)的圖象上,則n的值是( )
(k≠0)的圖象上.若正方形ABCD向左平移n個(gè)單位后,頂點(diǎn)C恰好落在反比例函數(shù)的圖象上,則n的值是( )
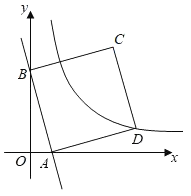
A.2B.3C.4.D.5
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
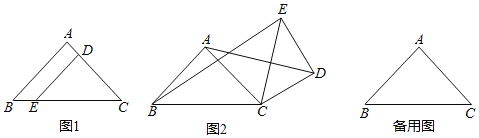
【題目】如圖1,在Rt△ABC中,∠BAC=90°,AB=AC,D,E兩點(diǎn)分別在AC,BC上,且DE∥AB,將△CDE繞點(diǎn)C按順時(shí)針?lè)较蛐D(zhuǎn),記旋轉(zhuǎn)角為α.
(1)問(wèn)題發(fā)現(xiàn):當(dāng)α=0°時(shí),![]() 的值為 ;
的值為 ;
(2)拓展探究:當(dāng)0°≤α<360°時(shí),若△EDC旋轉(zhuǎn)到如圖2的情況時(shí),求出![]() 的值;
的值;
(3)問(wèn)題解決:當(dāng)△EDC旋轉(zhuǎn)至A,B,E三點(diǎn)共線(xiàn)時(shí),若設(shè)CE=5,AC=4,直接寫(xiě)出線(xiàn)段BE的長(zhǎng) .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某校根據(jù)學(xué)校實(shí)際,決定開(kāi)設(shè)![]() :籃球、
:籃球、![]() :乒乓球、
:乒乓球、![]() :聲樂(lè)、
:聲樂(lè)、![]() :健美操四種活動(dòng)項(xiàng)目(必選且只能選一個(gè)),為了解學(xué)生最喜歡哪一種活動(dòng)項(xiàng)目,隨機(jī)抽取了部分學(xué)生進(jìn)行調(diào)查,并將調(diào)查結(jié)果整理后會(huì)制成如圖所示的不完整的統(tǒng)計(jì)圖.請(qǐng)你根據(jù)圖中提供的信息回答下列問(wèn)題:
:健美操四種活動(dòng)項(xiàng)目(必選且只能選一個(gè)),為了解學(xué)生最喜歡哪一種活動(dòng)項(xiàng)目,隨機(jī)抽取了部分學(xué)生進(jìn)行調(diào)查,并將調(diào)查結(jié)果整理后會(huì)制成如圖所示的不完整的統(tǒng)計(jì)圖.請(qǐng)你根據(jù)圖中提供的信息回答下列問(wèn)題:
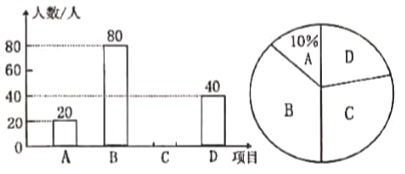
(1)求這次被調(diào)查的學(xué)生共有多少人;
(2)通過(guò)計(jì)算補(bǔ)全條形統(tǒng)計(jì)圖;
(3)已知該校有學(xué)生1600人,請(qǐng)根據(jù)調(diào)查結(jié)果估計(jì)該校最喜歡乒乓球的學(xué)生人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:對(duì)于線(xiàn)段![]() 和點(diǎn)
和點(diǎn)![]() ,當(dāng)
,當(dāng)![]() ,且
,且![]() 時(shí),稱(chēng)點(diǎn)
時(shí),稱(chēng)點(diǎn)![]() 為線(xiàn)段
為線(xiàn)段![]() 的“等距點(diǎn)”.特別地,當(dāng)
的“等距點(diǎn)”.特別地,當(dāng)![]() ,且
,且![]() 時(shí),稱(chēng)點(diǎn)
時(shí),稱(chēng)點(diǎn)![]() 為線(xiàn)段
為線(xiàn)段![]() 的“強(qiáng)等距點(diǎn)”.在平面直角坐標(biāo)系
的“強(qiáng)等距點(diǎn)”.在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .
.
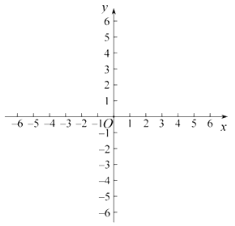
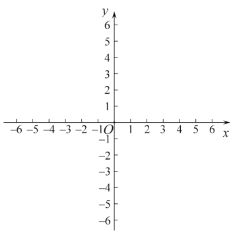
(1)有4個(gè)點(diǎn):![]() ,
,![]() ,
,![]() ,
,![]() .線(xiàn)段
.線(xiàn)段![]() 的“等距點(diǎn)”是 ;其中線(xiàn)段
的“等距點(diǎn)”是 ;其中線(xiàn)段![]() 的“強(qiáng)等距點(diǎn)”是 .
的“強(qiáng)等距點(diǎn)”是 .
(2)設(shè)第四象限有一點(diǎn)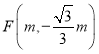 ,點(diǎn)
,點(diǎn)![]() 是線(xiàn)段
是線(xiàn)段![]() 的“強(qiáng)等距點(diǎn)”.
的“強(qiáng)等距點(diǎn)”.
①當(dāng)![]() 時(shí),求點(diǎn)
時(shí),求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②當(dāng)點(diǎn)![]() 又為線(xiàn)段
又為線(xiàn)段![]() 的“等距點(diǎn)”時(shí),求
的“等距點(diǎn)”時(shí),求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
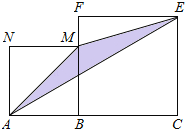
【題目】如圖,線(xiàn)段AC=n+1(其中n為正整數(shù)),點(diǎn)B在線(xiàn)段AC上,在線(xiàn)段AC同側(cè)作正方形ABMN及正方形BCEF,連接AM、ME、EA得到△AME.當(dāng)AB=1時(shí),△AME的面積記為S1;當(dāng)AB=2時(shí),△AME的面積記為S2;當(dāng)AB=3時(shí),△AME的面積記為
S3;則S3﹣S2= .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】定義:如圖1,對(duì)于直線(xiàn)![]() 同側(cè)的
同側(cè)的![]() 、
、![]() 兩點(diǎn),若在
兩點(diǎn),若在![]() 上的點(diǎn)
上的點(diǎn)![]() 滿(mǎn)足
滿(mǎn)足![]() ,則稱(chēng)
,則稱(chēng)![]() 為
為![]() 、
、![]() 兩點(diǎn)在
兩點(diǎn)在![]() 上的反射點(diǎn),
上的反射點(diǎn),![]() 與
與![]() 的和稱(chēng)為
的和稱(chēng)為![]() 、
、![]() 兩點(diǎn)的反射距離.
兩點(diǎn)的反射距離.

(1)如圖2,在邊長(zhǎng)為2的正方形![]() 中,
中,![]() 為
為![]() 的中點(diǎn),
的中點(diǎn),![]() 為
為![]() 、
、![]() 兩點(diǎn)在直線(xiàn)
兩點(diǎn)在直線(xiàn)![]() 上的反射點(diǎn),求
上的反射點(diǎn),求![]() 、
、![]() 兩點(diǎn)的反射距離;
兩點(diǎn)的反射距離;
(2)如圖3,![]() 內(nèi)接于
內(nèi)接于![]() ,直徑
,直徑![]() 為4,
為4,![]() ,點(diǎn)
,點(diǎn)![]() 為劣弧
為劣弧![]() 上一動(dòng)點(diǎn),點(diǎn)
上一動(dòng)點(diǎn),點(diǎn)![]() 為
為![]() 、
、![]() 兩點(diǎn)在
兩點(diǎn)在![]() 上的反射點(diǎn),當(dāng)
上的反射點(diǎn),當(dāng)![]() 、
、![]() 兩點(diǎn)的反射距離最大時(shí),求劣弧
兩點(diǎn)的反射距離最大時(shí),求劣弧![]() 的長(zhǎng);
的長(zhǎng);
(3)如圖4,在平面直角坐標(biāo)系中,拋物線(xiàn)![]() 與
與![]() 軸正半軸交于點(diǎn)
軸正半軸交于點(diǎn)![]() ,頂點(diǎn)為
,頂點(diǎn)為![]() ,若點(diǎn)
,若點(diǎn)![]() 為點(diǎn)
為點(diǎn)![]() 、
、![]() 在
在![]() 上的反射點(diǎn),同時(shí)點(diǎn)
上的反射點(diǎn),同時(shí)點(diǎn)![]() 為點(diǎn)
為點(diǎn)![]() 、
、![]() 在
在![]() 上的反射點(diǎn).
上的反射點(diǎn).
①請(qǐng)判斷線(xiàn)段![]() 和
和![]() 的位置關(guān)系,并給出證明;
的位置關(guān)系,并給出證明;
②求![]() 、
、![]() 兩點(diǎn)的反射距離與
兩點(diǎn)的反射距離與![]() 、
、![]() 兩點(diǎn)的反射距離的比值.
兩點(diǎn)的反射距離的比值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在![]() 中,
中, ![]() ,將直角三角板的直角頂點(diǎn)與
,將直角三角板的直角頂點(diǎn)與![]() 邊的中點(diǎn)
邊的中點(diǎn)![]() 重合,直角三角板繞著點(diǎn)
重合,直角三角板繞著點(diǎn)![]() 旋轉(zhuǎn),兩條直角邊分別交
旋轉(zhuǎn),兩條直角邊分別交![]() 邊于
邊于![]() ,則
,則![]() 的最小值是____.
的最小值是____.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com