
【題目】如圖,在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.點P從點A出發沿AB方向向點B運動,速度為1cm/s,同時點Q從點B出發沿B→C→A方向向點A運動,速度為2cm/s.當一個動點到達終點時,另一個動點也隨之停止運動.設運動時間為t(s).
(1)當t為何值時,△APC為等腰三角形.
(2)當點Q在線段BC上運動時,△PBQ的面積為S(cm2),寫出S與t之間的函數關系.
(3)當點Q在線段BC上運動時,是否存在某一時刻t,使S△PBQ:S四邊形APQC=5:3?若存在,求出t值;若不存在,說明理由.
(4)在運動過程中,是否存在某一時刻t,使BQ平分∠ABC?若存在,求出t的值;若不存在,請說明理由.
【答案】
(1)解:①當AP=PB時,∵∠ACB=90°,
∴CP=PA=PB,
∴t=5,
②當AC=AP時,t=8,
∴t=5s或8s時,△APC是等腰三角形
(2)解:當點Q在邊BC上運動時,過點Q作QH⊥AB于H,
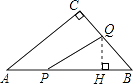
∵AP=xcm,
∴BP=(10﹣x)cm,BQ=2xcm,
∵△QHB∽△ACB,
∴ ![]() =
= ![]() ,
,
∴QH= ![]() xcm,
xcm,
y= ![]() BPQH=
BPQH= ![]() (10﹣x)
(10﹣x) ![]() x=﹣
x=﹣ ![]() x2+8x(0<x≤3)
x2+8x(0<x≤3)
(3)解:存在.∵S△PBQ:S四邊形APQC=5:3,
∴﹣ ![]() x2+8x=
x2+8x= ![]() ×
× ![]() ×6×8,
×6×8,
解得x= ![]() 或
或 ![]() ,
,
∴t= ![]() s或
s或 ![]() s時,S△PBQ:S四邊形APQC=5:3
s時,S△PBQ:S四邊形APQC=5:3
(4)解:存在.如圖作QH⊥AB于H.
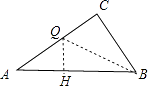
∵∠QBC=∠QBA,QC⊥BC,QH⊥AB,
∴QC=QH=2t﹣6,AQ=14﹣2t,
∵∠A=∠A,∠AHQ=∠C=90°,
∴△AQH∽△ABC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴t= ![]() ,
,
∴t= ![]() s時,BQ平分∠ABC
s時,BQ平分∠ABC
【解析】(1)分兩種情形討論求解①當AP=PB時,可以證明CP=PA=PB,t=5,.②當AC=AP時;t=5,t=5s或8s時,△APC是等腰三角形
(2)當點Q在邊BC上運動時,過點Q作QH⊥AB于H,由△QHB∽△ACB,推出 QHAC=QBAB 可得QH的長度, 根據y= 12 BPQH,列出式子即可;
(3)存在.由S△PBQ:S四邊形APQC=5:3,可得關于x的方程,解方程即可解決問題;
(4)存在.如圖作QH⊥AB于H.首先得出QC=QH=2t-6,AQ=14﹣2t,由△ AQH∽△ABC,可得 AQAB=QHBC ,從而列出方程, 解方程即可解決問題;
【考點精析】關于本題考查的三角形的面積和相似三角形的判定與性質,需要了解三角形的面積=1/2×底×高;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() 的角平分線與邊
的角平分線與邊![]() 交于點
交于點![]() ,
,![]() 的角平分線交直線
的角平分線交直線![]() 于點
于點![]() .
.
(1)若點![]() 在四邊形
在四邊形![]() 的內部,
的內部,
①如圖,若![]() ,
,![]() ,
,![]() ,則
,則![]() _______°;
_______°;
②如圖,試探索![]() 、
、![]() 、
、![]() 之間的數量關系,并將你的探索過程寫下來.
之間的數量關系,并將你的探索過程寫下來.
(2)如圖,若點![]() 是四邊形
是四邊形![]() 的外部,請你直接寫出
的外部,請你直接寫出![]() 、
、![]() 、
、![]() 之間的數量關系.
之間的數量關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程組解應用題:
為了保護環境,深圳某公交公司決定購買一批共10臺全新的混合動力公交車,現有A、B兩種型號,其中每臺的價格,年省油量如下表:
A | B | |
價格(萬元/臺) | a | b |
節省的油量(萬升/年) | 2.4 | 2 |
經調查,購買一臺A型車比購買一臺B型車多20萬元,購買2臺A型車比購買3臺B型車少60萬元.
(1)請求出a和b;
(2)若購買這批混合動力公交車每年能節省22.4萬汽油,求購買這批混合動力公交車需要多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】完成下面推理過程:

如圖,已知∠1 =∠2,∠B =∠C,可推得AB∥CD.理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(______________ _________),
∴∠2 =∠CGD(等量代換).
∴CE∥BF(___________________ ________).
∴∠ =∠C(__________________________).
又∵∠B =∠C(已知),
∴∠ =∠B(等量代換).
∴AB∥CD(________________________________).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,輪船沿正南方向以33海里/時的速度勻速航行,在m處觀測到燈塔p在西偏南69°方向下,航行2小時后到達n處,觀測燈塔p在西偏南57°方向上,若該船繼續向南航行至離燈塔最近位置,求此時輪船離燈塔的距離約為多少海里?(結果精確到整數,參考數據:tan33°≈ ![]() ,sin33°≈
,sin33°≈ ![]() ,cos33°≈
,cos33°≈ ![]() ,tan21°≈
,tan21°≈ ![]() ,sin21°≈
,sin21°≈ ![]() ,c0s21°≈
,c0s21°≈ ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,把直角三角形![]() 的直角頂點
的直角頂點![]() 放在直線
放在直線![]() 上,射線
上,射線![]() 平分
平分![]() .
.
(1)如圖,若![]() ,求
,求![]() 的度數.
的度數.
(2)若![]() ,則
,則![]() 的度數為 .
的度數為 .
(3)由(1)和(2),我們發現![]() 和
和![]() 之間有什么樣的數量關系?
之間有什么樣的數量關系?
(4)若將三角形![]() 繞點
繞點![]() 旋轉到如圖所示的位置,試問
旋轉到如圖所示的位置,試問![]() 和
和![]() 之間的數量關系是否發生變化?請說明理由.
之間的數量關系是否發生變化?請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, 在平面直角坐標系xOy中,三角形ABC三個頂點的坐標分別為(-2,-2),(3,1),(0,2),若把三角形ABC向上平移 3 個單位長度,再向左平移 ![]() 個單位長度得到三角形
個單位長度得到三角形 ![]() ,點A,B,C的對應點分別為
,點A,B,C的對應點分別為 ![]() ,
,![]() ,
,![]() .
.
(1)寫出點 ![]() ,
,![]() ,
,![]() 的坐標;
的坐標;
(2)在圖中畫出平移后的三角形 ![]() ;
;
(3)三角形 ![]() 的面積為__________.
的面積為__________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com