
【題目】某中學為了預測本校應屆畢業女生“一分鐘跳繩”項目考試情況,從九年級隨機抽取部分女生進行該項目測試,并以測試數據為樣本,繪制出如圖10所示的部分頻數分布直方圖(從左到右依次分為六個小組,每小組含最小值,不含最大值)和扇形統計圖.根據統計圖提供的信息解答下列問題:
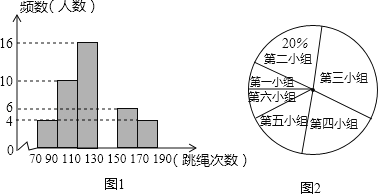
(1)補全頻數分布直方圖,并指出這個樣本數據的中位數落在第 小組;
(2)若測試九年級女生“一分鐘跳繩”次數不低于130次的成績為優秀,本校九年級女生共有260人,請估計該校九年級女生“一分鐘跳繩”成績為優秀的人數;
(3)如測試九年級女生“一分鐘跳繩”次數不低于170次的成績為滿分,在這個樣本中,從成績為優秀的女生中任選一人,她的成績為滿分的概率是多少?
【答案】(1)、三;(2)、104人;(3)、0.2
【解析】
試題分析:(1)、根據第二小組占比20%求出總人數,然后求出第四小組的人數,補全頻數直方圖;(2)、用總人數×優秀的比例即可求解;(3)、用滿分的人數÷優秀的人數即可得出滿分的概率.
試題解析:(1)、總人數是:10÷20%=50(人), 則第四組的人數是:50﹣4﹣10﹣16﹣6﹣4=10,
故中位數位于第三組;
(2)、該校九年級女生“一分鐘跳繩”成績為優秀的人數是:(50-4-10-16)÷50×260=104(人);
(3)、成績是優秀的人數是:10+6+4=20(人), 成績為滿分的人數是4,
則從成績為優秀的女生中任選一人,她的成績為滿分的概率是![]() =0.2.
=0.2.


科目:初中數學 來源: 題型:
【題目】如圖,已知MB=ND,∠MBA=∠NDC,下列條件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將下列方格紙中的△ABC向右平移7格,再向下平移2格,得到△![]() .(1)畫出平移后的三角形;
.(1)畫出平移后的三角形;
(2)若AB=5,則![]() = .
= .
(3)連接AA1,BB1, 根據“圖形平移”的性質,得:線段AA1與線段BB1的數量關系和位置關系是: .
(4)求圖中∠![]() AC+∠
AC+∠![]() BC的度數.
BC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】萬達旅行社為吸引市民組團去黃山風景區旅游,推出了如下的收費標準:

宿州高鐵新區組織員工去黃山風景區旅游,共支付給萬達旅行社旅游費用27 000元,請問該單位這次共有多少員工去黃山風景區旅游?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線MN與直線PQ垂直相交于O,點A在射線OP上運動,點B 在射線OM上運動.
(1)如圖1,已知AE、BE分別是∠BAO和∠ABO角的平分線,點A、B在運動的過程中,∠AEB的大小是否會發生變化?若發生變化,請說明變化的情況;若不發生變化,試求出∠AEB的大小.
(2)如圖2,已知AB不平行CD,AD、BC分別是∠BAP和∠ABM的角平分線,AD、BC的延長線交于點F,點A、B在運動的過程中,∠F= °;DE、CE又分別是∠ADC和∠BCD的角平分線,點A、B在運動的過程中,∠CED的大小也不發生變化,其大小為∠CED= °.
(3)如圖3,延長BA至G,已知∠BAO、∠OAG的角平分線與∠BOQ的角平分線及其延長線相交于E、F,則∠EAF= ° ;在△AEF中,如果有一個角是另一個角的3倍,則∠ABO= °.

查看答案和解析>>
科目:初中數學 來源: 題型:
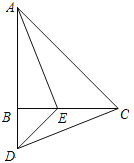
【題目】如圖,在△ABC中,AB=CB,∠ABC=90°,D為AB延長線上一點,點E在BC邊上,且BE=BD,連結AE、DE、DC.
① 求證:△ABE≌△CBD;
② 若∠CAE=30°,求∠BDC的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個港口相距72千米,一艘輪船從甲港出發,順流航行3小時到達乙港,休息1小時后立即返回;一艘快艇在輪船出發2小時后從乙港出發,逆流航行2小時到甲港,并立即返回(掉頭時間忽略不計)。已知水流速度是2千米/時,下圖表示輪船和快艇距甲港的距離y(千米)與輪船出發時間x(小時)之間的函數關系式,結合圖象解答下列問題:
(順流速度=船在靜水中速度+水流速度;逆流速度=船在靜水中速度-水流速度)

(1)輪船在靜水中的速度是 千米/時;快艇在靜水中的速度是 千米/時;
(2)求快艇返回時的解析式,寫出自變量取值范圍;
(3)快艇出發多長時間,輪船和快艇在返回途中相距12千米?(直接寫出結果)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中, ![]() 是邊長為
是邊長為![]() 的等邊三角形,直線
的等邊三角形,直線![]() 與
與![]() 軸、
軸、![]() 、
、![]() 分別交于點
分別交于點![]() 、
、![]() 、
、![]() .
. ![]() ,過點
,過點![]() 作
作![]() ,交
,交![]() 于點
于點![]() .
.
(![]() )點
)點![]() 的坐標為__________.(結果保留根號)
的坐標為__________.(結果保留根號)
(![]() )求證:點
)求證:點![]() 、
、![]() 關于
關于![]() 軸對稱.
軸對稱.
(![]() )若
)若![]() ,求直線
,求直線![]() 對應的函數表達式.
對應的函數表達式.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從3,0,-1,-2,-3這五個數中,隨機抽取一個數,作為函數y=(5-m2)x和關于x的方程(m+1)x2+mx+1=0中m的值,恰好使所得函數的圖象經過第一、三象限,且方程有實數根的概率為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com