
【題目】為了豐富同學們的課余生活,某學校舉行“親近大自然”戶外活動,現隨機抽取了部分學生進行主題為“你最想去的景點是?”的問卷調查,要求學生只能從“A(植物園),B(花卉園),C(濕地公園),D(森林公園)”四個景點中選擇一項,根據調查結果,繪制了如下兩幅不完整的統計圖.
請解答下列問題:
(1)本次調查的樣本容量是;
(2)補全條形統計圖;
(3)若該學校共有3600名學生,試估計該校最想去濕地公園的學生人數.
【答案】
(1)60
(2)
解:選擇C的人數為:60﹣15﹣10﹣12=23(人),
補全條形圖如圖:

(3)
![]() ×3600=1380(人
×3600=1380(人![]() )
)
答:估計該校最想去濕地公園的學生人數約由1380人![]()
【解析】解:(1)本次調查的樣本容量是15÷25%=60;
故答案為:60.
(1)由A的人數及其人數占被調查人數的百分比可得;(2)根據各項目人數之和等于總數可得C選項的人數;(3)用樣本中最想去濕地公園的學生人數占被調查人數的比例乘總人數即可.此題主要考查了條形統計圖和扇形統計圖的綜合運用,讀懂統計圖,從不同的統計圖中得到必要的信息是解決問題的關鍵.條形統計圖能清楚地表示出每個項目的數據;扇形統計圖直接反映部分占總體的百分比大小.


科目:初中數學 來源: 題型:
【題目】如圖,P是等邊三角形ABC內一點,將線段AP繞點A順時針旋轉60°得到線段AQ,連接BQ.若PA=6,PB=8,PC=10,則四邊形APBQ的面積為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】聊城“水城之眼”摩天輪是亞洲三大摩天輪之一,也是全球首座建筑與摩天輪相結合的城市地標,如圖,點O是摩天輪的圓心,長為110米的AB是其垂直地面的直徑,小瑩在地面C點處利用測角儀測得摩天輪的最高點A的仰角為33°,測得圓心O的仰角為21°,則小瑩所在C點到直徑AB所在直線的距離約為(tan33°≈0.65,tan21°≈0.38)( )
A.169米
B.204米
C.240米
D.407米
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景區7月1日﹣7月7日一周天氣預報如圖,小麗打算選擇這期間的一天或兩天去該景區旅游,求下列事件的概率:
(1)隨機選擇一天,恰好天氣預報是晴;
(2)隨機選擇連續的兩天,恰好天氣預報都是晴.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AC=6,BC=8,點F在邊AC上,并且CF=2,點E為邊BC上的動點,將△CEF沿直線EF翻折,點C落在點P處,則點P到邊AB距離的最小值是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景:
如圖①,在四邊形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究線段AC,BC,CD之間的數量關系.
小吳同學探究此問題的思路是:將△BCD繞點D,逆時針旋轉90°到△AED處,點B,C分別落在點A,E處(如圖②),易證點C,A,E在同一條直線上,并且△CDE是等腰直角三角形,所以CE= ![]() CD,從而得出結論:AC+BC=
CD,從而得出結論:AC+BC= ![]() CD.
CD.
簡單應用:
(1)在圖①中,若AC= ![]() ,BC=2
,BC=2 ![]() ,則CD= .
,則CD= .
(2)如圖③,AB是⊙O的直徑,點C、D在⊙上, ![]() =
= ![]() ,若AB=13,BC=12,求CD的長.
,若AB=13,BC=12,求CD的長.
拓展規律:
(3)如圖④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的長(用含m,n的代數式表示)
(4)如圖⑤,∠ACB=90°,AC=BC,點P為AB的中點,若點E滿足AE= ![]() AC,CE=CA,點Q為AE的中點,則線段PQ與AC的數量關系是 .
AC,CE=CA,點Q為AE的中點,則線段PQ與AC的數量關系是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在RT△ABC中,∠C=90°,BC=3cm,AC=4cm,以點C為圓心,以2.5cm為半徑畫圓,則⊙C與直線AB的位置關系是( )
A.相交
B.相切
C.相離
D.不能確定
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在四張背面完全相同的紙牌A、B、C、D,其中正面分別畫有四個不同的幾何圖形(如圖),小華將這4張紙牌背面朝上洗勻后摸出一張,放回洗勻后再摸一張.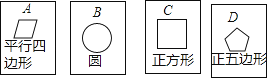
(1)用樹狀圖(或列表法)表示兩次摸牌所有可能出現的結果(紙牌可用A、B、C、D表示);
(2)求摸出兩張紙牌牌面上所畫幾何圖形,既是軸對稱圖形又是中心對稱圖形的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com