
【題目】已知∠AOB是一個直角,作射線OC,再分別作∠AOC和∠BOC的平分線OD、OE.
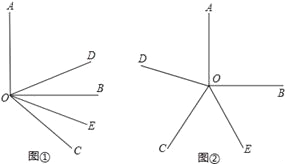
(1)如圖①,當∠BOC=70°時,求∠DOE的度數;
(2)如圖②,當射線OC在∠AOB內繞O點旋轉時,∠DOE的大小是否發生變化若變化,說明理由;若不變,求∠DOE的度數;
(3)如圖③,當射線OC在∠AOB外繞O點旋轉時,畫出圖形,判斷∠DOE的大小是否發生變化若變化,說明理由;若不變,求∠DOE的度數.

【答案】(1)∠DOE=45°;(2)∠DOE的大小不變等于45°.理由見解析;(3)∠DOE的大小發生變化,∠DOE=45°或135.
【解析】試題分析:(1)根據角平分線的定義,OD、OE分別平分∠AOC和∠BOC,則可求得∠COE、∠COD的值,∠DOE=∠COE+∠COD;
(2)結合角的特點,∠DOE=∠DOC+∠COE,求得結果進行判斷和計算;
(3)正確作出圖形,判斷大小變化.
試題解析:
解:(1)∵OD、OE分別平分∠AOC和∠BOC,
∴∠COE=![]() ∠COB=35°,∠COD=
∠COB=35°,∠COD=![]() ∠AOC=10°,
∠AOC=10°,
∴∠DOE=45°;
(2)∠DOE的大小不變等于45°.
理由:∠DOE=∠DOC+∠COE=![]() ∠COB+
∠COB+![]() ∠AOC
∠AOC
=![]() (∠COB+∠AOC)
(∠COB+∠AOC)
=![]() ∠AOB=45°;
∠AOB=45°;
(3)∠DOE的大小發生變化,∠DOE=45°或135.
如圖①,∠DOE=45°;
如圖②,∠DOE=135°.(說理過程同(2))
點睛: 此題主要考查了角平分線的性質以及角的有關計算,正確作圖,熟記角的特點與角平分線的定義是解決此題的關鍵.


科目:初中數學 來源: 題型:
【題目】(1)已知在△ABC中,∠A=90°,∠B=67.5°,請畫一條直線,把這個三角形分割成兩個等腰三角形(請你選用下面給出的備用圖,把所有不同的分割方法都畫出來.只需畫圖,不必說明理由,但要在圖中標出相等兩角的度數).
(2)已知在△ABC中,∠C是其最小的內角,過頂點B的一條直線把這個三角形分割成了兩個等腰三角形,請探求∠ABC與∠C之間的關系.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=AC,點F是BC延長線上一點,以CF為邊,作菱形CDEF,使菱形CDEF與點A在BC的同側,連接BE,點G是BE的中點,連接AG、DG.
(1)如圖①,當∠BAC=∠DCF=90°時,直接寫出AG與DG的位置和數量關系;
(2)如圖②,當∠BAC=∠DCF=60°時,試探究AG與DG的位置和數量關系,
(3)當∠BAC=∠DCF=α時,直接寫出AG與DG的數量關系.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com