Question

如圖，點I是△ABC的內心，AI交邊BC于點E，交△ABC的外接圓于點D．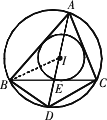

求證：(1)DB＝DI；

(2)ID²＝DE·AD．

Answer 1

答案：
解析：

分析：(1)連接BI．根據三角形內心的性質及圓周角的性質，可找出相關角之間的關系，從而使結論獲證； 　　(2)利用(1)的結論將問題轉化為DB2＝DE·AD，只需證明△DBE∽△DAB即可． 　　證明：(1)連接BI．因為點I是△ABC的內心，所以∠ABI＝∠IBC，∠BAD＝∠CAD．又因為∠DBC＝∠CAD，所以∠BAD＝∠DBC．所以∠BID＝∠BAD＋∠ABI＝∠DBC＋∠IBC＝∠DBI，即∠BID＝∠DBI．所以DB＝DI． 　　(2)由(1)知，∠DBC＝∠BAD． 　　又∠BDE＝∠ADB，所以△DBE∽△DAB． 　　所以，即DB2＝DE·DA． 　　由(1)知，DB＝DI，所以ID2＝DE·AD． 　　點評：試題中往往將三角形的內心和外接圓、相似等知識結合在一起來考查同學們綜合運用知識的能力，因此平時要注意培養分析解題的能力．