
【題目】根據題意計算與解答
(1)計算(x﹣y)2﹣(x﹣2y)(x+y)
(2)若關于x,y的二元一次方程組 ![]() 的解滿足x+y>﹣
的解滿足x+y>﹣ ![]() ,求出滿足條件的m的所有正整數值.
,求出滿足條件的m的所有正整數值.
(3)若關于x的方程 ![]() +
+ ![]() =3的解為正數,求m的取值范圍.
=3的解為正數,求m的取值范圍.
【答案】
(1)解:原式=x2﹣2xy+y2﹣x2+xy+2y2=﹣xy+3y2
(2)解: ![]() ,
,
① +②得:x+y=﹣m+2,
代入不等式得:﹣m+2>﹣ ![]() ,
,
解得:m< ![]() ,
,
則正整數解為1,2
(3)解:去分母得:x+m﹣3m=3x﹣9,
解得:x= ![]() ,
,
由分式方程有正數解,得到 ![]() >0,且
>0,且 ![]() ≠3,
≠3,
解得:m< ![]() 且m≠
且m≠ ![]()
【解析】(1)原式利用完全平方公式,以及多項式乘以多項式法則計算,去括號合并即可得到結果;(2)方程組兩方程相加表示出x+y,代入已知不等式求出m的范圍,即可確定出正整數解;(3)分式方程去分母轉化為整式方程,由分式方程解為正數,求出m的范圍即可.
【考點精析】掌握二元一次方程組的解和分式方程的解是解答本題的根本,需要知道二元一次方程組中各個方程的公共解,叫做這個二元一次方程的解;分式方程無解(轉化成整式方程來解,產生了增根;轉化的整式方程無解);解的正負情況:先化為整式方程,求整式方程的解.


 藍天教育暑假優化學習系列答案
藍天教育暑假優化學習系列答案科目:初中數學 來源: 題型:
【題目】某市水果批發部門欲將A市的一批水果運往本市銷售,有火車和汽車兩種運輸方式,運輸過程中的損耗均為200元/時。其它主要參考數據如下:
運輸工具 | 途中平均速度(千米/時) | 運費(元/千米) | 裝卸費用(元) |
火車 | 100 | 15 | 2000 |
汽車 | 80 | 20 | 900 |
(1)如果汽車的總支出費用比火車費用多1100元,你知道本市與A市之間的路程是多少千米嗎?請你列方程解答.
(2)如果A市與某市之間的距離為S千米,且知道火車與汽車在路上耽誤的時間分別為2小時和3.1小時,你若是某市水果批發部門的經理,要將這種水果從A市運往本市銷售。你將選擇哪種運輸方式比較合算呢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某計算裝置有一數據輸入口A和一運算結果的輸出口B,表格中是小明輸入的一些數據和這些數據經該裝置計算后輸出的相應結果,按照這個計算裝置的計算規律,若輸入的數是10,則輸出的數是( )
A | 1 | 2 | 3 | 4 | 5 |
B | 0 | 3 | 8 | 15 | 24 |
A. 99 B. 100 C. 101 D. 102
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】元旦晚會上,王老師要為她的學生及班級的六位科任老師送上賀年卡,網上購買賀年卡的優惠條件是:購買50或50張以上享受團購價.王老師發現:零售價與團購價的比是5:4,王老師計算了一下,按計劃購買賀年卡只能享受零售價,如果比原計劃多購買6張賀年卡就能享受團購價,這樣她正好花了100元,而且比原計劃還節約10元錢;
(1)賀年卡的零售價是多少?
(2)班里有多少學生?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線PA經過點A(-1,0)、點P(1,2),直線PB是一次函數y=-x+3的圖象.
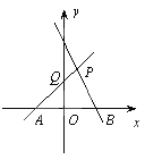
(1)求直線PA的表達式及Q點的坐標;
(2)求四邊形PQOB的面積;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,點E、F分別在直線AB,CD上,點P在AB、CD之間,連結EP、FP,如圖1,過FP上的點G作GH∥EP,交CD于點H,且∠1=∠2.
(1)求證:AB∥CD;
(2)如圖2,將射線FC沿FP折疊,交PE于點J,若JK平分∠EJF,且JK∥AB,則∠BEP與∠EPF之間有何數量關系,并證明你的結論;
(3)如圖3,將射線FC沿FP折疊,將射線EA沿EP折疊,折疊后的兩射線交于點M,當EM⊥FM時,求∠EPF的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】①在數軸上沒有點能表示![]() +1;②無理數是開不盡方的數;③存在最小的實數;④4的平方根是±2,用式子表示是
+1;②無理數是開不盡方的數;③存在最小的實數;④4的平方根是±2,用式子表示是![]() =±2;⑤某數的絕對值,相反數,算術平方根都是它本身,則這個數是0,其中正確的是______.
=±2;⑤某數的絕對值,相反數,算術平方根都是它本身,則這個數是0,其中正確的是______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com