
【題目】已知拋物線![]() 的對稱軸是直線
的對稱軸是直線![]() 且與
且與![]() 軸相交于
軸相交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() 點
點![]() 的坐標為
的坐標為![]() .
.
![]() 求拋物線的解析式;
求拋物線的解析式;
![]() 若點
若點![]() 是第一象限內拋物線上一點,過點
是第一象限內拋物線上一點,過點![]() 作直線
作直線![]() 軸于點
軸于點![]() 交直線
交直線![]() 于點
于點![]() 當
當![]() 時,求四邊形
時,求四邊形![]() 的面積.
的面積.
![]() 在
在![]() 的條件下,若點
的條件下,若點![]() 在拋物線上,點
在拋物線上,點![]() 在拋物線的對稱軸上,當以點
在拋物線的對稱軸上,當以點![]() 為頂點的四邊形是平行四邊形時,求出所有符合條件的點
為頂點的四邊形是平行四邊形時,求出所有符合條件的點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)滿足條件的點
;(3)滿足條件的點![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]()
【解析】
(1)根據拋物線![]() 的對稱軸是直線
的對稱軸是直線![]() ,點
,點![]() 在拋物線上,列出方程組,求得
在拋物線上,列出方程組,求得![]() 中字母的值,即可得到拋物線的解析式.
中字母的值,即可得到拋物線的解析式.
(2)先根據拋物線的解析式,得到點![]() 、點
、點![]() 的坐標;再由點
的坐標;再由點![]() 、點
、點![]() 的坐標,得到直線
的坐標,得到直線![]() 的解析式;設點
的解析式;設點![]() 的坐標為
的坐標為![]() ,得
,得![]() ,
,![]() ,根據已知條件
,根據已知條件![]() ,列出方程,通過解方程求得未知數,得到
,列出方程,通過解方程求得未知數,得到![]() 、
、![]() ,
,![]() 三點坐標,根據三角形面積公式,結合圖1,利用割補法求面積,即有
三點坐標,根據三角形面積公式,結合圖1,利用割補法求面積,即有![]() ,即可得到答案.
,即可得到答案.
(3)設點![]() 的坐標為
的坐標為![]() ,分三種情況進行討論:
,分三種情況進行討論:![]() 如圖2,當
如圖2,當![]() 為對角線時,點
為對角線時,點![]() 的坐標為
的坐標為![]() ;
;![]() 如圖3,當
如圖3,當![]() 為對角線時,點
為對角線時,點![]() 的坐標為
的坐標為![]() ;
;![]() 如圖4.當
如圖4.當![]() 為對角線時,點
為對角線時,點![]() 的坐標為
的坐標為![]() ,分別將點
,分別將點![]() 的坐標代入
的坐標代入![]() ,即得到三個不同的點
,即得到三個不同的點![]() .
.
解:(1)∵點![]() 的坐標為
的坐標為![]() ,對稱軸是直線
,對稱軸是直線![]() ,
,
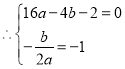
解得![]()
![]() 拋物線的解析式為
拋物線的解析式為![]() .
.
(2)畫出圖形,如圖1所示,
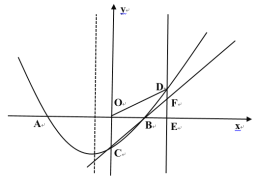
圖1
令![]() ,代入
,代入![]() ,
,
解得![]() ,
,![]() ,
,
∵點![]() 的坐標為
的坐標為![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ,
,
令![]() ,代入
,代入![]() ,得
,得![]() ,
,
∴點![]() 的坐標為
的坐標為![]() ,
,
可求得直線![]() 的解析式為
的解析式為![]() .
.
設點![]() 的坐標為
的坐標為![]() ,
,
則![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,
∴![]() .
.
(3)設點![]() 的坐標為
的坐標為![]() ,
,
![]() 如圖2,當
如圖2,當![]() 為對角線時,點
為對角線時,點![]() 的坐標為
的坐標為![]() ,
,
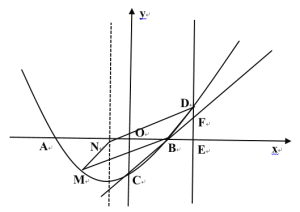
圖2
將點![]() 坐標代入
坐標代入![]() 得,
得,![]() ,
,
此時點![]() 的坐標為
的坐標為![]() ;
;
![]() 如圖3,當
如圖3,當![]() 為對角線時,點
為對角線時,點![]() 的坐標為
的坐標為![]() ,
,
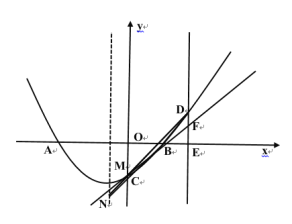
圖3
將點![]() 坐標代入
坐標代入![]() 得,
得, ![]() ,
,
此時點![]() 的坐標為
的坐標為![]() ;
;
![]() 如圖4.當
如圖4.當![]() 為對角線時,點
為對角線時,點![]() 的坐標為
的坐標為![]() ,
,
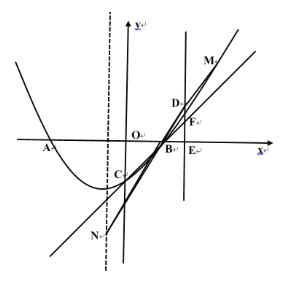
圖4
將點![]() 坐標代入
坐標代入![]() 得,
得,![]() ,
,
此時點![]() 的坐標為
的坐標為![]() .
.
綜上所述,滿足條件的點![]() 的坐標為
的坐標為![]() 或
或![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
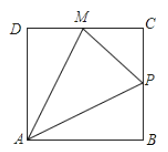
【題目】如圖,點P按A→B→C→M的順序在邊長為l的正方形邊上運動,M是CD邊上中點,設點P經過的路程x為自變量,△APM的面積為y,則函數y的大致圖像是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解2012年全國中學生創新能力大賽中競賽項目“知識產權”筆試情況,隨機抽查了部分參賽同學的成績,整理并制作圖表如下:
分數段 | 頻數 | 頻率 |
60≤x<70 | 30 | 0.1 |
70≤x<80 | 90 | n |
80≤x<90 | m | 0.4 |
90≤x≤100 | 60 | 0.2 |

請根據以上圖表提供的信息,解答下列問題:
(1)本次調查的樣本容量為 ;
(2)在表中:m= .n= ;
(3)補全頻數分布直方圖:
(4)參加比賽的小聰說,他的比賽成績是所有抽查同學成績的中位數,據此推斷他的成績落在 分數段內;
(5)如果比賽成績80分以上(含80分)為優秀,那么你估計該競賽項目的優秀率大約是
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了了解某校九年級學生的課外數學學習時長情況,該校將選取部分學生進行調查,以下樣本中,最具代表性的是( )
A.該年級籃球社團的學生
B.該年級數學成績前![]() 名的女生
名的女生
C.該年級跑步較快的學生
D.從每個班級中,抽取學號為![]() 的整數倍的學生
的整數倍的學生
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD中,AB∥x軸,AB=6.點A的坐標為(1,﹣4),點D的坐標為(﹣3,4),點B在第四象限,點G是AD與y軸的交點,點P是CD邊上不與點C,D重合的一個動點,過點P作y軸的平行線PM,過點G作x軸的平行線GM,它們相交于點M,將△PGM沿直線PG翻折,當點M的對應點落在坐標軸上時,點P的坐標為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=﹣x2+4x+5圖象的頂點為D,對稱軸是直線1,一次函數y![]() x+1的圖象與x軸交于點A,且與直線DA關于l的對稱直線交于點B.
x+1的圖象與x軸交于點A,且與直線DA關于l的對稱直線交于點B.
(1)點D的坐標是 ;
(2)直線l與直線AB交于點C,N是線段DC上一點(不與點D、C重合),點N的縱坐標為n.過點N作直線與線段DA、DB分別交于點P、Q,使得△DPQ與△DAB相似.
①當n![]() 時,求DP的長;
時,求DP的長;
②若對于每一個確定的n的值,有且只有一個△DPQ與△DAB相似,請直接寫出n的取值范圍 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與
與![]() 交于點
交于點![]() ,將點
,將點![]() 向右平移某個距離得到點
向右平移某個距離得到點![]() ,點
,點![]() 在拋物線上.已知點
在拋物線上.已知點![]() ,
,![]() .
.
(1) 當![]() 時.
時.
①求點![]() 的坐標(用含
的坐標(用含![]() 的式子表示);
的式子表示);
②求線段![]() 的長度;
的長度;
(2)若拋物線與線段![]() 恰有一個公共點,結合函數圖象,求
恰有一個公共點,結合函數圖象,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
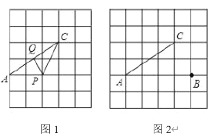
【題目】在每個小正方形的邊長為1的網格中,點![]() ,
,![]() ,
,![]() 均在格點上,點
均在格點上,點![]() ,
,![]() 分別為線段
分別為線段![]() ,
,![]() 上的動點.
上的動點.
(I)如圖(1),當點![]() ,
,![]() 分別為
分別為![]() ,
,![]() 中點時,
中點時,![]() 的值為__________;
的值為__________;
(Ⅱ)當![]() 取得最小值時,在如圖(2)所示的網格中,用無刻度的真尺,畫出線段
取得最小值時,在如圖(2)所示的網格中,用無刻度的真尺,畫出線段![]() ,
,![]() ,簡要說明點
,簡要說明點![]() 和點
和點![]() 的位置是如何找到的(不要求證明)__________.
的位置是如何找到的(不要求證明)__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com