
【題目】如圖,在Rt△ABC中,∠ACB=90°,AC=BC=2,以點A為圓心,AC的長為半徑作 ![]() 交AB于點E,以點B為圓心,BC的長為半徑作
交AB于點E,以點B為圓心,BC的長為半徑作 ![]() 交AB于點D,則陰影部分的面積為 .
交AB于點D,則陰影部分的面積為 . 
 激活思維優(yōu)加課堂系列答案
激活思維優(yōu)加課堂系列答案 活力試卷系列答案
活力試卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,△ABC中,A點坐標為(2,4),B點坐標為(﹣3,﹣2),C點坐標為(3,1).

(1)在圖中畫出△ABC關(guān)于y軸對稱的△A′B′C′(不寫畫法),并寫出點A′,B′,C′的坐標;
(2)求△ABC的面積.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖①,△ABC與△CDE是等腰直角三角形,直角邊AC、CD在同一條直線上,點M、N分別是斜邊AB、DE的中點,點P為AD的中點,連接AE、BD.
(1)猜想PM與PN的數(shù)量關(guān)系及位置關(guān)系,請直接寫出結(jié)論;
(2)現(xiàn)將圖①中的△CDE繞著點C順時針旋轉(zhuǎn)α(0°<α<90°),得到圖②,AE與MP、BD分別交于點G、H.請判斷(1)中的結(jié)論是否成立?若成立,請證明;若不成立,請說明理由;
(3)若圖②中的等腰直角三角形變成直角三角形,使BC=kAC,CD=kCE,如圖③,寫出PM與PN的數(shù)量關(guān)系,并加以證明.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】探究與發(fā)現(xiàn):
探究一:我們知道,三角形的一個外角等于與它不相鄰的兩個內(nèi)角的和.那么,三角形的一個內(nèi)角與它不相鄰的兩個外角的和之間存在何種數(shù)量關(guān)系呢?
已知:如圖1,∠FDC與∠ECD分別為△ADC的兩個外角,試探究∠A與∠FDC+∠ECD的數(shù)量關(guān)系為:____________________(直接寫出結(jié)果).
探究二:三角形的一個內(nèi)角與另兩個內(nèi)角的平分線所夾的鈍角之間有何種關(guān)系?
已知:如圖2,在△ADC中,DP,CP分別平分∠ADC和∠ACD,試探究∠P與∠A的數(shù)量關(guān)系為:____________________(直接寫出結(jié)果).
探究三:若將△ADC改為任意四邊形ABCD呢?
已知:如圖3,在四邊形ABCD中,DP,CP分別平分∠ADC和∠BCD,試利用上述結(jié)論探究∠P與∠A+∠B的數(shù)量關(guān)系.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
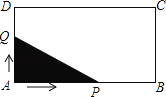
【題目】如圖,長方形ABCD中,AB=8,AD=4.點Q與點P同時從點A出發(fā),點Q以每秒1個單位的速度沿A→D→C→B的方向運動,點P以每秒3個單位的速度沿A→B→C→D的方向運動,當P,Q兩點相遇時,它們同時停止運動.設(shè)Q點運動的時間為x(秒),在整個運動過程中,當△APQ為直角三角形時,則相應(yīng)的x的值或取值范圍是_______________.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】閱讀下列材料:
我們知道![]() 的幾何意義是在數(shù)軸上數(shù)
的幾何意義是在數(shù)軸上數(shù)![]() 對應(yīng)的點與原點的距離,即
對應(yīng)的點與原點的距離,即![]() =
=![]() ,也就是說,
,也就是說,![]() 表示在數(shù)軸上數(shù)
表示在數(shù)軸上數(shù)![]() 與數(shù)0對應(yīng)的點之間的距離;這個結(jié)論可以推廣為
與數(shù)0對應(yīng)的點之間的距離;這個結(jié)論可以推廣為![]() 表示在數(shù)軸上數(shù)
表示在數(shù)軸上數(shù)![]() 與數(shù)
與數(shù)![]() 對應(yīng)的點之間的距離;
對應(yīng)的點之間的距離;
例1.解方程|![]() |=2.因為在數(shù)軸上到原點的距離為2的點對應(yīng)的數(shù)為
|=2.因為在數(shù)軸上到原點的距離為2的點對應(yīng)的數(shù)為![]() ,所以方程|
,所以方程|![]() |=2的解為
|=2的解為![]() .
.
例2.解不等式|![]() -1|>2.在數(shù)軸上找出|
-1|>2.在數(shù)軸上找出|![]() -1|=2的解(如圖),因為在數(shù)軸上到1對應(yīng)的點的距離等于2的點對應(yīng)的數(shù)為-1或3,所以方程|
-1|=2的解(如圖),因為在數(shù)軸上到1對應(yīng)的點的距離等于2的點對應(yīng)的數(shù)為-1或3,所以方程|![]() -1|=2的解為
-1|=2的解為![]() =-1或
=-1或![]() =3,因此不等式|
=3,因此不等式|![]() -1|>2的解集為
-1|>2的解集為![]() <-1或
<-1或![]() >3.
>3.
![]()
例3.解方程|![]() -1|+|
-1|+|![]() +2|=5.由絕對值的幾何意義知,該方程就是求在數(shù)軸上到1和-2對應(yīng)的點的距離之和等于5的點對應(yīng)的
+2|=5.由絕對值的幾何意義知,該方程就是求在數(shù)軸上到1和-2對應(yīng)的點的距離之和等于5的點對應(yīng)的![]() 的值.因為在數(shù)軸上1和-2對應(yīng)的點的距離為3(如圖),滿足方程的
的值.因為在數(shù)軸上1和-2對應(yīng)的點的距離為3(如圖),滿足方程的![]() 對應(yīng)的點在1的右邊或-2的左邊.若
對應(yīng)的點在1的右邊或-2的左邊.若![]() 對應(yīng)的點在1的右邊,可得
對應(yīng)的點在1的右邊,可得![]() =2;若
=2;若![]() 對應(yīng)的點在-2的左邊,可得
對應(yīng)的點在-2的左邊,可得![]() =-3,因此方程|
=-3,因此方程|![]() -1|+|
-1|+|![]() +2|=5的解是
+2|=5的解是![]() =2或
=2或![]() =-3.
=-3.
![]()
參考閱讀材料,解答下列問題:
(1)方程|![]() +3|=4的解為 ;
+3|=4的解為 ;
(2)解不等式:|![]() -3|≥5;
-3|≥5;
(3)解不等式:|![]() -3|+|
-3|+|![]() +4|≥9
+4|≥9
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
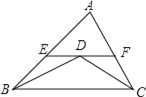
【題目】如圖,△ABC中,BD平分∠ABC,CD平分∠ACB,過點D作EF∥BC,與AB、AC分別相交于E、F,若已知AB=9,AC=7,求△AEF的周長.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】填空并完成以下證明:
已知:點P在直線CD上,∠BAP+∠APD=180°,∠1=∠2.
求證:AB∥CD,∠E=∠F.
證明:∵∠BAP+∠APD=180°,(已知)
∴AB∥ .( )
∴∠BAP= .( )
又∵∠1=∠2,(已知)
∠3= ﹣∠1,
∠4= ﹣∠2,
∴∠3= (等式的性質(zhì))
∴AE∥PF.( )
∴∠E=∠F.( )

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com