
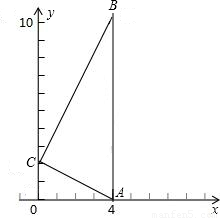
 解:如圖,①當點C在原點(0,0)與(0,10)時是直角三角形;
解:如圖,①當點C在原點(0,0)與(0,10)時是直角三角形;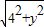 ,
,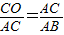 ,
,

 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 坐標原點.A、B兩點的橫坐標分別是方程x2-4x-12=0的兩根,且cos∠DAB=
坐標原點.A、B兩點的橫坐標分別是方程x2-4x-12=0的兩根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 18、在平面直角坐標系中,把一個圖形先繞著原點順時針旋轉的角度為θ,再以原點為位似中心,相似比為k得到一個新的圖形,我們把這個過程記為【θ,k】變換.例如,把圖中的△ABC先繞著原點O順時針旋轉的角度為90°,再以原點為位似中心,相似比為2得到一個新的圖形△A1B1C1,可以把這個過程記為【90°,2】變換.
18、在平面直角坐標系中,把一個圖形先繞著原點順時針旋轉的角度為θ,再以原點為位似中心,相似比為k得到一個新的圖形,我們把這個過程記為【θ,k】變換.例如,把圖中的△ABC先繞著原點O順時針旋轉的角度為90°,再以原點為位似中心,相似比為2得到一個新的圖形△A1B1C1,可以把這個過程記為【90°,2】變換.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com