
【題目】如圖,矩形ABCD中,AB=4,AD=3,M是邊CD上一點,將△ADM沿直線AM對折,得到△ANM.
(1)當AN平分∠MAB時,求DM的長;
(2)連接BN,當DM=1時,求△ABN的面積;
(3)當射線BN交線段CD于點F時,求DF的最大值.

【答案】(1)DM=![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)由折疊可知:△ANM≌△ADM,∠MAN=∠DAM,由AN平分∠MAB,得到∠MAN=∠NAB,進一步有∠DAM=∠MAN=∠NAB.由四邊形ABCD是矩形,得到∠DAM=30°,由DM=ADtan∠DAM得到DM的長;
(2)如圖1,延長MN交AB延長線于點Q,∵由四邊形ABCD是矩形,得到∠DMA=∠MAQ.由折疊可知:△ANM≌△ADM,∠DMA=∠AMQ,得到∠MAQ=∠AMQ,故MQ=AQ.
設NQ=x,則AQ=MQ=1+x.在Rt△ANQ中,由![]() ,得到x=4.
,得到x=4.
故NQ=4,AQ=5,由![]() =
=![]() =
=![]() ANNQ,即可得到結論;
ANNQ,即可得到結論;
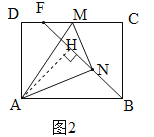
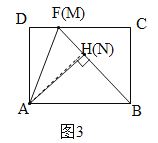
(3)如圖2,過點A作AH⊥BF于點H,則△ABH∽△BFC,故![]() .由AH≤AN=3,AB=4,故當點N、H重合(即AH=AN)時,DF最大.此時M、F重合,B、N、M三點共線,△ABH≌△BFC(如圖3),而CF=BH=
.由AH≤AN=3,AB=4,故當點N、H重合(即AH=AN)時,DF最大.此時M、F重合,B、N、M三點共線,△ABH≌△BFC(如圖3),而CF=BH=![]() =
=![]() ,故課求出DF的最大值.
,故課求出DF的最大值.
試題解析:(1)由折疊可知:△ANM≌△ADM,∴∠MAN=∠DAM,∵AN平分∠MAB,∴∠MAN=∠NAB,∴∠DAM=∠MAN=∠NAB.∵四邊形ABCD是矩形,∴∠DAB=90°,∴∠DAM=30°,∴DM=ADtan∠DAM=![]() =
=![]() ;
;
(2)如圖1,延長MN交AB延長線于點Q,∵四邊形ABCD是矩形,∴AB∥DC,∴∠DMA=∠MAQ.由折疊可知:△ANM≌△ADM,∴∠DMA=∠AMQ,AN=AD=3,MN=MD=1,∴∠MAQ=∠AMQ,∴MQ=AQ.
設NQ=x,則AQ=MQ=1+x.在Rt△ANQ中, ![]() ,∴
,∴![]() ,解得:x=4.
,解得:x=4.
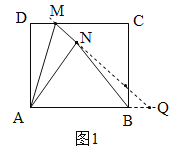
∴NQ=4,AQ=5,∵AB=4,AQ=5,∴![]() =
==
![]() ANNQ=
ANNQ=![]() ;
;
(3)如圖2,過點A作AH⊥BF于點H,則△ABH∽△BFC,∴![]() .∵AH≤AN=3,AB=4,∴當點N、H重合(即AH=AN)時,DF最大.(AH最大,BH最小,CF最小,DF最大)
.∵AH≤AN=3,AB=4,∴當點N、H重合(即AH=AN)時,DF最大.(AH最大,BH最小,CF最小,DF最大)
此時M、F重合,B、N、M三點共線,△ABH≌△BFC(如圖3),∴CF=BH=![]() =
=![]() =
=![]() ,∴DF的最大值為:
,∴DF的最大值為:![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖過刨平的木板上的兩個點,能彈出一條筆直的墨線,而且只能彈出一條墨線,能解釋這一實際應用的數學知識是( ) 
A.兩點確定一條直線
B.兩點之間線段最短
C.垂線段最短
D.在同一平面內,過一點有且只有一條直線與已知直線垂直
查看答案和解析>>
科目:初中數學 來源: 題型:
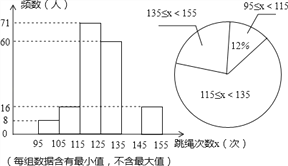
【題目】在我市開展的“陽光體育”跳繩活動中,為了了解中學生跳繩活動的開展情況,隨機抽查了全市八年級部分同學1分鐘跳繩的次數,將抽查結果進行統計,并繪制兩個不完整的統計圖.請根據圖中提供的信息,解答下列問題:
(1)本次共抽查了多少名學生?
(2)請補全頻數分布直方圖空缺部分,直接寫出扇形統計圖中跳繩次數范圍135≤x≤155所在扇形的圓心角度數.
(3)若本次抽查中,跳繩次數在125次以上(含125次)為優秀,請你估計全市8000名八年級學生中有多少名學生的成績為優秀?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖:在平行四邊形ABCD中,對角線AC與BD交于點O,過點O的直線EF分別與AD、BC交于點E、F,EF⊥AC,連結AF、CE.
(1)求證:OE=OF;
(2)請判斷四邊形AECF是什么特殊四邊形,請證明你的結論.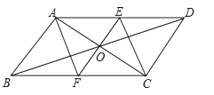
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校數學興趣小組開展了一次課外活動,過程如下:如圖①,正方形ABCD中,AB=4,將三角板放在正方形ABCD上,使三角板的直角頂點與D點重合.三角板的一邊交AB于點P,另一邊交BC的延長線于點Q.
(1)求證:AP=CQ;
(2)如圖②,小明在圖1的基礎上作∠PDQ的平分線DE交BC于點E,連接PE,他發現PE和QE存在一定的數量關系,請猜測他的結論并予以證明;
(3)在(2)的條件下,若AP=1,求PE的長.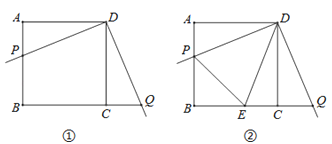
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com