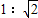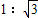Question

等邊三角形的內切圓半徑和外接圓半徑之比為（ ）
A．
B．1：2
C．
D．1：3

Answer 1

【答案】分析：作出輔助線OD、OE，證明△AOD為直角三角形且∠OAD為30°，即可求出OD、OA的比．
解答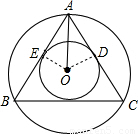：解：如圖，連接OD、OE；
因為AB、AC切圓O于E、D，
所以OE⊥AB，OD⊥AC；
又因為AO=AO，
EO=DO，
所以△AEO≌△ADO（HL），
故∠DAO=∠EAO；
又∵△ABC為等邊三角形，
∴∠BAC=60°，
∴∠OAC=60°×=30°，
∴OD：AO=1：2．
故選B．
點評：此題將等邊三角形的內切圓半徑和外接圓半徑綜合考查，找到直角三角形，將三角形內切圓和三角形外接圓聯系起來是解題的關鍵．