
 時,求出此二次函數的解析式;
時,求出此二次函數的解析式;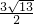 ?若存在,求出P點坐標;若不存在,請說明理由.
?若存在,求出P點坐標;若不存在,請說明理由. ,
, .
. ,
,
 AB•|y0|=
AB•|y0|=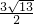
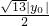 =
=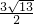
 來進行計算.
來進行計算.

 課程達標測試卷闖關100分系列答案
課程達標測試卷闖關100分系列答案 新卷王期末沖刺100分系列答案
新卷王期末沖刺100分系列答案 全能闖關100分系列答案
全能闖關100分系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 已知二次函數y=-x2+2x+m的部分圖象如圖所示,則關于x的一元二次方程-x2+2x+m=0的解為( )
已知二次函數y=-x2+2x+m的部分圖象如圖所示,則關于x的一元二次方程-x2+2x+m=0的解為( )| A、x1=1,x2=3 | B、x1=0,x2=3 | C、x1=-1,x2=1 | D、x1=-1,x2=3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 已知二次函數y=-x2+bx+c的圖象如圖所示,它與x軸的一個交點坐標為(-1,0),與y軸的交點坐標為(0,3).
已知二次函數y=-x2+bx+c的圖象如圖所示,它與x軸的一個交點坐標為(-1,0),與y軸的交點坐標為(0,3).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com