
【題目】小松想利用所學數學知識測量學校旗桿高度,如圖,旗桿AB的頂端垂下一繩子,將繩子拉直釘在地上,末端恰好在C處且與地面成60°角,小松拿起繩子末端,后退至E處,并拉直繩子,此時繩子末端D距離地面2m且繩子與水平方向成45°角.求旗桿AB的高度.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】魔術師說將你想到的數進行以下四步操作,我就可以猜到你心里想的數.
第一步:心中想一個數,求其平方;
第二步:想比這個數小2的數,求其平方;
第三步:求其平方的差值;
第四步:平方的差值除以4再加1.
將結果告訴我,我就能猜中你心里想的數.
(1)若你想的數是5,求出你告訴魔術師的結果是多少.
(2)聰明的同學們,你覺得魔術師的步驟一定能猜中你心中的數嗎?請用代數式計算證明你的結論.
解答:魔術師 猜中你心中的數(填“能”或“否”);
證明:設心中想的數為![]() (
(![]() 為任意實數)
為任意實數)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,拋物線y=ax2+bx+c(a≠0)與x軸交于點A(-2,0)、B(1,0),直線x=![]() 與此拋物線交于點C,與x軸交于點M,在直線上取點D,使MD=MC,連接AC,BC,AD,BD,某同學根據圖象寫出下列結論:①a-b=0;②當x<
與此拋物線交于點C,與x軸交于點M,在直線上取點D,使MD=MC,連接AC,BC,AD,BD,某同學根據圖象寫出下列結論:①a-b=0;②當x<![]() 時,y隨x增大而增大;③四邊形ACBD是菱形;④9a-3b+c>0.你認為其中正確的是
時,y隨x增大而增大;③四邊形ACBD是菱形;④9a-3b+c>0.你認為其中正確的是

A. ②③④ B. ①②③ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 交
交![]() 軸于
軸于![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() 直線
直線![]() 經過點
經過點![]() .
.
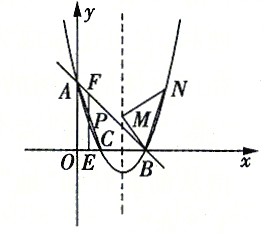
(1)求拋物線的解析式;
(2)點![]() 是直線
是直線![]() 下方的拋物線上一動點,過點
下方的拋物線上一動點,過點![]() 作
作![]() 軸于點
軸于點![]() 交直線
交直線![]() 于點
于點![]() 設點
設點![]() 的橫坐標為
的橫坐標為![]() 若
若![]() 求
求![]() 的值;
的值;
(3)![]() 是第一象限對稱軸右側拋物線上的一點,連接
是第一象限對稱軸右側拋物線上的一點,連接![]() 拋物線的對稱軸上是否存在點
拋物線的對稱軸上是否存在點![]() .使得
.使得![]() 與
與![]() 相似,且
相似,且![]() 為直角,若存在,請直接寫出點
為直角,若存在,請直接寫出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
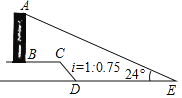
【題目】如圖,AB是一垂直于水平面的建筑物,某同學從建筑物底端B出發,先沿水平方向向右行走20米到達點C,再經過一段坡度(或坡比)為i=1:0.75、坡長為10米的斜坡CD到達點D,然后再沿水平方向向右行走40米到達點E(A,B,C,D,E均在同一平面內),在E處處測得建筑物頂端A的仰角為24°,則建筑物AB的高度約為__米.(參考數據:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,一次函數y=mx+n(m≠0)的圖象與y軸交于點C,與反比例函數y=![]() (k≠0)的圖象交于A,B兩點,點A在第一象限,縱坐標為4,點B在第三象限,BM⊥x軸,垂足為點M,BM=OM=2.
(k≠0)的圖象交于A,B兩點,點A在第一象限,縱坐標為4,點B在第三象限,BM⊥x軸,垂足為點M,BM=OM=2.
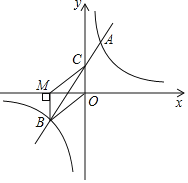
(1)求反比例函數和一次函數的解析式.
(2)連接OB,MC,求四邊形MBOC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
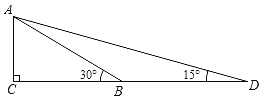
【題目】構建幾何圖形解決代數問題是“數形結合”思想的重要性,在計算tan15°時,如圖.在Rt△ACB中,∠C=90°,∠ABC=30°,延長CB使BD=AB,連接AD,得∠D=15°,所以tan15°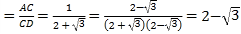 .類比這種方法,計算tan22.5°的值為( )
.類比這種方法,計算tan22.5°的值為( )
A.![]() B.
B.![]() ﹣1C.
﹣1C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業承接了27000件產品的生產任務,計劃安排甲、乙兩個車間的共50名工人,合作生產20天完成.已知甲、乙兩個車間利用現有設備,工人的工作效率為:甲車間每人每天生產25件,乙車間每人每天生產30件.
(1)求甲、乙兩個車間各有多少名工人參與生產?
(2)為了提前完成生產任務,該企業設計了兩種方案:
方案一 甲車間租用先進生產設備,工人的工作效率可提高20%,乙車間維持不變.
方案二 乙車間再臨時招聘若干名工人(工作效率與原工人相同),甲車間維持不變.
設計的這兩種方案,企業完成生產任務的時間相同.
①求乙車間需臨時招聘的工人數;
②若甲車間租用設備的租金每天900元,租用期間另需一次性支付運輸等費用1500元;乙車間需支付臨時招聘的工人每人每天200元.問:從新增加的費用考慮,應選擇哪種方案能更節省開支?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
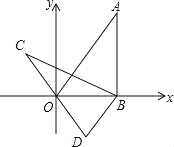
【題目】如圖,在平面直角坐標系xOy中,直線y=![]() x經過點A,作AB⊥x軸于點B,將△ABO繞點B逆時針旋轉60°得到△CBD,若點B的坐標為(2,0),則點C的坐標為 .
x經過點A,作AB⊥x軸于點B,將△ABO繞點B逆時針旋轉60°得到△CBD,若點B的坐標為(2,0),則點C的坐標為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com