已知y是x的二次函數,且其圖象在x軸上截得的線段AB長4個單位,當x=3時,y取得最小值-2.
(1)求這個二次函數的解析式;
(2)若此函數圖象上有一點P,使△PAB的面積等于12個平方單位,求P點坐標.
分析:(1)根據拋物線的對稱軸為x=3,以及AB=4,可求得A、B的坐標,然后根據其頂點坐標用頂點式二次函數通式設拋物線的解析式,然后將A或B點的坐標代入拋物線中即可求得二次函數的解析式.
(2)已知了AB的長,可根據三角形的面積求得P點縱坐標的絕對值,然后代入拋物線的解析式中即可求得P點的坐標.
解答: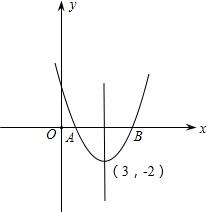
解:(1)∵當x=3時y取得最小值-2.
即拋物線頂點為(3,-2),對稱軸為直線x=3,
∴設二次函數解析式為y=a(x-3)
2-2.
又∵圖象在x軸上截得線段AB的長是4,
∴圖象與x軸交于(1,0)和(5,0)兩點.
∴a(1-3)
2-2=0,
∴a=
,
∴所求二次函數解析式為y=
x
2-3x+
.
(2)∵△PAB的面積為12個平方單位,|AB|=4.
∴
×4×|Py|=12,
∴|Py|=6,
∴Py=±6.
但拋物線開口向上,函數值最小為-2,
∴Py=-6應舍去,
∴Py=6又點P在拋物線上,
∴6=
x
2-3x+
,
解得,x
1=-1,x
2=7.
即點P的坐標為(-1,6)或(7,6).
點評:本題考查了二次函數解析式的確定以及圖形面積的求法等知識點.

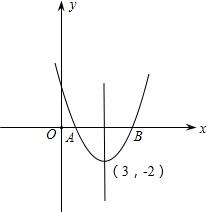 解:(1)∵當x=3時y取得最小值-2.
解:(1)∵當x=3時y取得最小值-2.
