
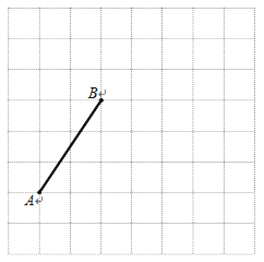
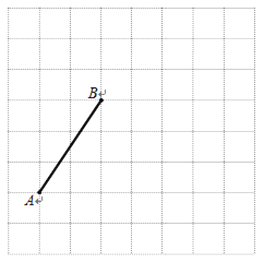
【題目】下圖是由邊長為1個單位長度的小正方形組成的網格,線段AB的端點在格點上.
(1)請建立適當的平面直角坐標系xOy,使得A點的坐標為(-3,-1),在此坐標系下,B點的坐標為________________;
(2)將線段BA繞點B逆時針旋轉90°得線段BC,畫出BC;在第(1)題的坐標系下,C點的坐標為__________________;
(3)在第(1)題的坐標系下,二次函數y=ax2+bx+c(a≠0)的圖象過O、B、C三點,則此函數圖象的對稱軸方程是________________.
【答案】 (-1,2) (2,0) x=1
【解析】分析:![]() 根據點
根據點![]() 的坐標建立坐標系,即可寫出點
的坐標建立坐標系,即可寫出點![]() 的坐標.
的坐標.
![]() 畫出點
畫出點![]() 旋轉后的對應點
旋轉后的對應點![]() 連接
連接![]() ,寫出點
,寫出點![]() 的坐標.
的坐標.
![]() 用待定系數法求出函數解析式,即可求出對稱軸方程.
用待定系數法求出函數解析式,即可求出對稱軸方程.
詳解:(1)建立坐標系如圖,
B點的坐標為![]() ;
;
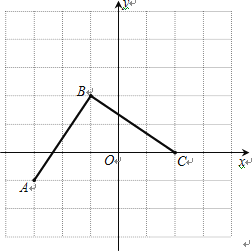
(2)線段BC如圖,C點的坐標為![]()
(3)把點![]() 代入二次函數
代入二次函數![]() ,得
,得
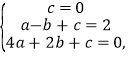
解得: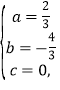
二次函數解析為:![]()
對稱軸方程為:![]()
故對稱軸方程是![]()
點睛:考查圖形與坐標;旋轉、對稱變換;待定系數法求二次函數解析式,二次函數的圖象與性質.熟練掌握各個知識點是解題的關鍵.
【題型】解答題
【結束】
18
【題目】特殊兩位數乘法的速算——如果兩個兩位數的十位數字相同,個位數字相加為10,那么能立說出這兩個兩位數的乘積.如果這兩個兩位數分別寫作AB和AC(即十位數字為A,個位數字分別為B、C,B+C=10,A>3),那么它們的乘積是一個4位數,前兩位數字是A和(A+1)的乘積,后兩位數字就是B和C的乘積.
如:47×43=2021,61×69=4209.
(1)請你直接寫出83×87的值;
(2)設這兩個兩位數的十位數字為x(x>3),個位數字分別為y和z(y+z=10),通過計算驗證這兩個兩位數的乘積為100x(x+1)+yz.
(3)99991×99999=___________________(直接填結果)
【答案】7221
【解析】分析:![]() 套用上面的歸納總結代入數據,即可得出結論;
套用上面的歸納總結代入數據,即可得出結論;
![]() 利用上面總結的結論套入數據表示出該兩個兩位數的成績,在將等式展開合并同類項得出左邊=右邊,從而證明結論成立.
利用上面總結的結論套入數據表示出該兩個兩位數的成績,在將等式展開合并同類項得出左邊=右邊,從而證明結論成立.
![]() 直接運算即可.
直接運算即可.
詳解:(1)83和87滿足題中的條件,即十位數都是8,8>3,且個位數字分別是3和7,之和為10,那么它們的乘積是一個4位數,前兩位數字是8和9的乘積,后兩位數字就是3和7的乘積,因而,答案為:7221.
(2) 這兩個兩位數的十位數字為x(x>3),個位數字分別為y和z,則由題知y+z=10,
因而有:(10x+y)(10x+z)=100x2+10xz+10xy+yz
=100x2+10x(y+z)+yz,
=100x2+100x+yz,
=100x(x+1)+yz.
(3)9999000009.


 奪冠訓練單元期末沖刺100分系列答案
奪冠訓練單元期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】如圖,一次函數的圖象與反比例函數的圖象交于A(﹣3,1)、B(m,3)兩點,
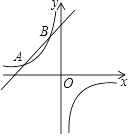
(1)求反比例函數和一次函數的解析式;
(2)寫出使一次函數的值大于反比例函數的x的取值范圍;
(3)連接AO、BO,求△ABO的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在菱形ABCD中,對角線AC、BD相交于點O,DE∥AC,AE∥BD.
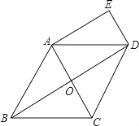
(1)求證:四邊形AODE是矩形;
(2)若AB=4,∠BCD=120°,求四邊形AODE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖, 在![]() 中,
中, ![]() ,
,![]() ,
,![]() ,P是邊BC上的一動點,過點P作PE⊥AB,垂足為E,延長PE至點Q,使PQ=PC, 聯結
,P是邊BC上的一動點,過點P作PE⊥AB,垂足為E,延長PE至點Q,使PQ=PC, 聯結![]() 交邊AB于點
交邊AB于點![]() .
.
(1)求AD的長;
(2)設![]() ,
,![]() 的面積為y, 求y關于x的函數解析式,并寫出定義域;
的面積為y, 求y關于x的函數解析式,并寫出定義域;
(3)過點C作![]() , 垂足為F, 聯結PF、QF, 試探索當點P在邊BC的什么位置時,
, 垂足為F, 聯結PF、QF, 試探索當點P在邊BC的什么位置時,![]() 為等邊三角形?請指出點P的位置并加以證明.
為等邊三角形?請指出點P的位置并加以證明.
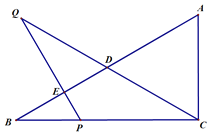
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB是⊙O的直徑,AC是⊙O的切線,BC交⊙O于點D(如圖1).
(1)若AB=2,∠B=30°,求CD的長;
(2) 取AC的中點E,連結D、E(如圖2),求證:DE與⊙O相切.

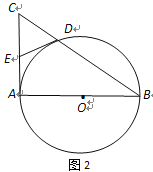
【答案】(1)![]() ;(2)見解析
;(2)見解析
【解析】分析:![]() 連接AD ,根據AC是⊙O的切線,AB是⊙O的直徑,得到∠CAB=∠ADB=90°,根據∠B=30°,解直角三角形求得
連接AD ,根據AC是⊙O的切線,AB是⊙O的直徑,得到∠CAB=∠ADB=90°,根據∠B=30°,解直角三角形求得![]() 的長度.
的長度.
![]() 連接OD,AD.根據DE=CE=EA,∠EDA=∠EAD. 根據OD=OA,得到
連接OD,AD.根據DE=CE=EA,∠EDA=∠EAD. 根據OD=OA,得到
∠ODA=∠DAO,得到∠EDA+∠ODA=∠EAD+∠DAO.得到∠EDO=90°即可.
詳解:(1)如圖,連接AD ,
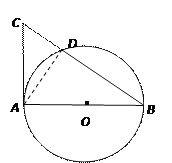
∵AC是⊙O的切線,AB是⊙O的直徑,
∴∠CAB=∠ADB=90°,
∴ΔCAB,ΔCAD均是直角三角形.
∴∠CAD=∠B=30°.
在RtΔCAB中,AC=ABtan30°=![]()
∴在RtΔCAD中,CD=ACsin30°=![]()
(2)如圖,連接OD,AD.

∵AC是⊙O的切線,AB是⊙O的直徑,
∴∠CAB=∠ADB=∠ADC=90°,
又∵E為AC中點,
∴DE=CE=EA,
∴∠EDA=∠EAD.
∵OD=OA,
∴∠ODA=∠DAO,
∴∠EDA+∠ODA=∠EAD+∠DAO.
即:∠EDO=∠EAO=90°.
又點D在⊙O上,因此DE與⊙O相切.
點睛:考查解直角三角形,圓周角定理,切線的判定與性質等,屬于圓的綜合題,比較基礎.注意切線的證明方法,是高頻考點.
【題型】解答題
【結束】
21
【題目】課外活動時間,甲、乙、丙、丁4名同學相約進行羽毛球比賽.
(1)如果將4名同學隨機分成兩組進行對打,求恰好選中甲乙兩人對打的概率;
(2)如果確定由丁擔任裁判,用“手心、手背”的方法在另三人中競選兩人進行比賽.競選規則是:三人同時伸出“手心”或“手背”中的一種手勢,如果恰好只有兩人伸出的手勢相同,那么這兩人上場,否則重新競選.這三人伸出“手心”或“手背”都是隨機的,求一次競選就能確定甲、乙進行比賽的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解不等式組: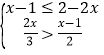 , 并把解集在數軸上表示出來.
, 并把解集在數軸上表示出來.
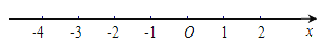
【答案】-3<x≤1
【解析】分析:分別解不等式,在數軸上表示出解集,找出解集的公共部分即可.
詳解: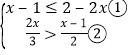 ,
,
解不等式①得:![]() ,
,
解不等式②得:![]()
∴原不等式組的解集為-3<x≤1
解集在數軸上表示為:

點睛:考查解一元一次不等式組,比較容易,分別解不等式,找出解集的公共部分即可.
【題型】解答題
【結束】
17
【題目】下圖是由邊長為1個單位長度的小正方形組成的網格,線段AB的端點在格點上.
(1)請建立適當的平面直角坐標系xOy,使得A點的坐標為(-3,-1),在此坐標系下,B點的坐標為________________;
(2)將線段BA繞點B逆時針旋轉90°得線段BC,畫出BC;在第(1)題的坐標系下,C點的坐標為__________________;
(3)在第(1)題的坐標系下,二次函數y=ax2+bx+c(a≠0)的圖象過O、B、C三點,則此函數圖象的對稱軸方程是________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
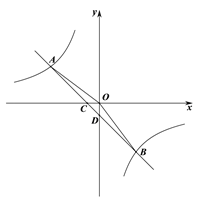
【題目】如圖,在平面直角坐標系中,一次函數的圖象與反比例函數圖象交于第二,四象限內A,B兩點,與![]() 軸交于點C,與
軸交于點C,與![]() 軸交于點D.若點B的縱坐標為
軸交于點D.若點B的縱坐標為![]() ,OA=5,
,OA=5, ![]() .
.
(1)求反比例函數解析式;
(2)求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察表格:
|
|
| |
1條直線 0個交點 平面分成(1+1)塊 | 2條直線 1個交點 平面分成(1+1+2)塊 | 3條直線 (1+2)個交點 平面分成(1+1+2+3)塊 | 4條直線 (1+2+3)個交點 平面分成(1+1+2+3+4)塊 |
根據表格中的規律解答問題:
(1)5條直線兩兩相交,有 個交點,平面被分成 塊;
(2)n條直線兩兩相交,有 個交點,平面被分成 塊;
(3)應用發現的規律解決問題:一張圓餅切10刀(不許重疊),最多可得到 塊餅.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小蟲從點A出發在一條直線上來回爬行,假定向右爬行的路程記為正數,向左爬行的路程記為負數,爬行的路程依次為:(單位:cm)①+5,②-3,③+10,④-8,⑤-6,⑥+11,⑦-9.
(1)小蟲最后是否回到出發點A,說明理由;
(2)小蟲在第幾次爬行后離點A最遠,此時距離點A多少厘米?
(3)在爬行過程中,如果每爬行1厘米獎勵一粒芝麻,那么小蟲一共得到多少粒芝麻?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com