
(1)如圖①,在正方形ABCD中,△AEF的頂點E,F分別在BC,CD邊上,高AG與正方形的邊長相等,求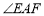 的度數.
的度數.
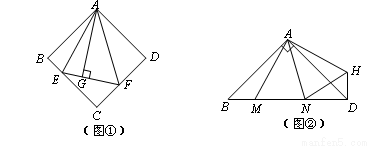
(2)如圖②,在Rt△ABD中,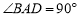 ,
,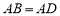 ,點M,N是BD邊上的任意兩點,且
,點M,N是BD邊上的任意兩點,且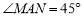 ,將△ABM繞點A逆時針旋轉
,將△ABM繞點A逆時針旋轉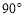 至△ADH位置,連接
至△ADH位置,連接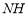 ,試判斷MN,ND,DH之間的數量關系,并說明理由.
,試判斷MN,ND,DH之間的數量關系,并說明理由.
(3)在圖①中,連接BD分別交AE,AF于點M,N,若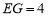 ,
,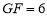 ,
,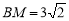 ,求AG,MN的長.
,求AG,MN的長.
(1) 45°.(2) MN2=ND2+DH2.理由見解析;(3)5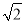 .
.
【解析】
試題分析:(1)根據高AG與正方形的邊長相等,證明三角形全等,進而證明角相等,從而求出解.
(2)用三角形全等和正方形的對角線平分每一組對角的知識可證明結論.
(3)設出線段的長,結合方程思想,用數形結合得到結果.
試題解析:(1)在Rt△ABE和Rt△AGE中,AB=AG,AE=AE,
∴Rt△ABE≌Rt△AGE(HL).
∴∠BAE=∠GAE.
同理,∠GAF=∠DAF.
∴∠EAF=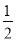 ∠BAD=45°.
∠BAD=45°.
(2)MN2=ND2+DH2.
∵∠BAM=∠DAH,∠BAM+∠DAN=45°,
∴∠HAN=∠DAH+∠DAN=45°.
∴∠HAN=∠MAN.
又∵AM=AH,AN=AN,
∴△AMN≌△AHN.
∴MN=HN.
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°.
∴∠HDN=∠HDA+∠ADB=90°.
∴NH2=ND2+DH2.
∴MN2=ND2+DH2.
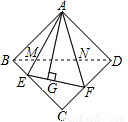
(3)由(1)知,BE=EG,DF=FG.
設AG=x,則CE=x-4,CF=x-6.
在Rt△CEF中,
∵CE2+CF2=EF2,
∴(x-4)2+(x-6)2=102.
解這個方程,得x1=12,x2=-2(舍去負根).
即AG=12.(8分)
在Rt△ABD中,
∴BD=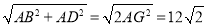 .
.
在(2)中,MN2=ND2+DH2,BM=DH,
∴MN2=ND2+BM2.
設MN=a,則a2=(12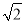 -3
-3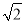 -a)2+(3
-a)2+(3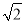 )2.
)2.
即a 2=(9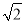 -a) 2+(3
-a) 2+(3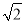 ) 2,
) 2,
∴a=5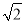 .即MN=5
.即MN=5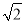 .
.
考點:1.正方形的性質;2.全等三角形的判定與性質;3.勾股定理.


 字詞句段篇系列答案
字詞句段篇系列答案科目:初中數學 來源:2014-2015學年福建省南平市八年級上學期期中考試數學試卷(解析版) 題型:選擇題
如圖A、B、C三個居民小區的位置成三角形,現決定三個小區之間修建一個超市,使它到三個小區的距離相等,則超市應建在( )

A.AC,BC 的兩條高線的交點處
B.∠A,∠B兩內角平分線的交點處
C.AC、BC兩邊中線的交點處
D.AC、BC兩條邊垂直平分線的交點處
查看答案和解析>>
科目:初中數學 來源:2014-2015學年福建省南平市八年級上學期期中考試數學試卷(解析版) 題型:解答題
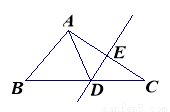
(8分)如圖,在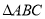 中,DE是AC的垂直平分線,AE=3cm,
中,DE是AC的垂直平分線,AE=3cm,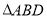 的周長為13cm,求
的周長為13cm,求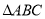 的周長
的周長
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com