解:(1)設發放樹苗點離A處x(0≤x≤700)米,所有學生到發放樹苗點的距離的和為y米,
則:①當0≤x≤300時,有y=20x+40(300-x)+30(700-x)=-50x+33000,
②當300<x≤700時,有y=20x+40(x-300)+30(700-x)=30x+9000,
①中x=300時,y有最小值18000,
②中y>18000,
∴按方案①設點,發放樹苗點應設在距離A處300米處,即B處.
(2)設發放樹苗點距離A處x(0≤x≤700)米,
則:①當0≤x≤300時,有:20x+30(700-x)=40(300-x),
解得x=-300(不合題意,舍去),
②當300<x≤700時,有:20x+30(700-x)=40(x-300),
解得:x=660,
∴按方案二設點,發放樹苗點應設在距離A處660米.
(3)設甲小組減小a(a<20)人,
由(2)得:(20-a)x+30(700-x)=40(x-300)(300<x≤700),
解得:

,
又∵
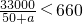
,且a越大,x越小
∴若甲小組減少人數則發放樹苗點離B處越來越近.
分析:(1)設發放樹苗點離A處x(0≤x≤700)米,所有學生到發放樹苗點的距離的和為y米,然后將x進行分段處理,分別得出最小值,從而可得出答案.
(2)設發放樹苗點距離A處x(0≤x≤700)米,根據甲組與丙組的所有學生到發放樹苗點距離的和等于乙組所有學生到發放樹苗點距離的和可列出方程,解出符合條件的解即可.
(3)設甲小組減小a(a<20)人,根據(2)的條件可列出方程,解出x的表達式即可作出說明.
點評:本題考查一次函數的應用,有一定的難度,解答此類題目的方法是根據題意所述的等價關系列出函數解析式,然后分段處理函數,得出符合題意的結果.

 ,
,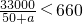 ,且a越大,x越小
,且a越大,x越小
