
【題目】如圖1,拋物線![]() 與
與![]() 鈾交于
鈾交于![]() ,與
,與![]() 軸交于
軸交于![]() 拋物線的頂點為
拋物線的頂點為![]() 直線
直線![]() 過
過![]() 交
交![]() 軸于
軸于![]() .
.
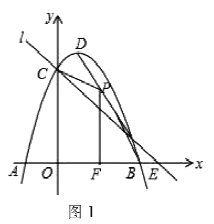
(1)寫出![]() 的坐標和直線
的坐標和直線![]() 的解析式;
的解析式;
(2)![]() 是線段
是線段![]() 上的動點(不與
上的動點(不與![]() 重合),
重合),![]() 軸于
軸于![]() 設四邊形
設四邊形![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 之間的兩數關系式,并求
之間的兩數關系式,并求![]() 的最大值;
的最大值;
(3)點![]() 在
在![]() 軸的正半軸上運動,過
軸的正半軸上運動,過![]() 作
作![]() 軸的平行線,交直線
軸的平行線,交直線![]() 于
于![]() 交拋物線于
交拋物線于![]() 連接
連接![]() ,將
,將![]() 沿
沿![]() 翻轉,
翻轉,![]() 的對應點為
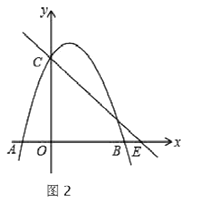
的對應點為![]() .在圖2中探究:是否存在點
.在圖2中探究:是否存在點![]() ;使得
;使得![]() 恰好落在
恰好落在![]() 軸?若存在,請求出
軸?若存在,請求出![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,當
,當![]() 時,
時,![]() 有最大值,最大值為
有最大值,最大值為![]() ;(3)存在.點
;(3)存在.點![]() 的坐標為
的坐標為![]() 或
或![]() .
.
【解析】
(1)先把拋物線解析式配成頂點式即可得到D點坐標,再求出C點坐標,然后利用待定系數法求直線l的解析式;
(2)先根據拋物線與x軸的交點問題求出B(3,0),再利用待定系數法求出直線BD的解析式為y=-2x+6,則P(x,-2x+6),然后根據梯形的面積公式可得![]() ,再利用二次函數的性質求S的最大值;
,再利用二次函數的性質求S的最大值;
(3)如圖2,設Q(t,0)(t>0),則可表示出![]() ,利用兩點間的距離公式得到
,利用兩點間的距離公式得到![]() ,
,![]() ,然后證明NM=CM得到
,然后證明NM=CM得到![]() ,再解絕對值方程求滿足條件的t的值,從而得到點Q的坐標.
,再解絕對值方程求滿足條件的t的值,從而得到點Q的坐標.
![]() ,
,
![]()
當![]() 時,
時,![]()
則![]() ,
,
設直線![]() 的解析式為
的解析式為![]() ,
,
把分別![]() 代入得
代入得![]()
解得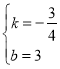 ,
,
![]() 直線
直線![]() 的解析式為
的解析式為![]() ;
;
![]() 當
當![]() 時,
時,![]() ,
,
解得![]() ,
,
則![]()
設直線![]() 的解析式為
的解析式為![]()
把![]() 分別代入得
分別代入得![]() ,
,
解得![]() ,
,
![]() 直線
直線![]() 的解析式為
的解析式為![]()
則![]() ,
,
![]()
![]() ,
,
![]() 當
當![]() 時,
時,![]() 有最大值,最大值為
有最大值,最大值為![]() ;
;
![]() 存在.
存在.
如圖2,設![]() ,
,
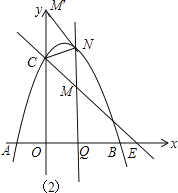
則![]()
![]()
![]() ,
,
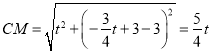 ,
,
![]() 沿
沿![]() 翻轉,
翻轉,![]() 的對應點為
的對應點為![]() 落在
落在![]() 軸上,
軸上,
![]() ,
,
∵![]() 軸,
軸,
![]()
![]()
![]()
![]()
![]()
當![]() ,
,
解得![]() (舍去),
(舍去),![]() ,
,
此時![]() 點坐標為
點坐標為![]() ;
;
當![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
此時![]() 點坐標為
點坐標為![]() ,
,
綜上所述:點![]() 的坐標為
的坐標為![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 的圖象經過A(-1,0)、B(4,5)三點.
的圖象經過A(-1,0)、B(4,5)三點.
(1)求此二次函數的解析式;
(2)當x為何值時,y隨x的增大而減小?
(3)當x為何值時,y>0?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:在以![]() 為原點的平面直角坐標系中,拋物線的頂點為
為原點的平面直角坐標系中,拋物線的頂點為![]() 點,且經過點
點,且經過點![]() ,
,![]() ,
,![]() 三點.
三點.
(1)求直線![]() 和該拋物線相應的函數表達式;
和該拋物線相應的函數表達式;
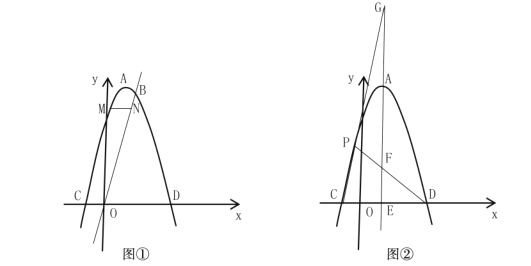
(2)如圖①,點![]() 為拋物線上的一個動點,且在直線
為拋物線上的一個動點,且在直線![]() 的上方,過點
的上方,過點![]() 作
作![]() 軸的平行線與直線
軸的平行線與直線![]() 交于點
交于點![]() ,求
,求![]() 的最大值.
的最大值.
(3)如圖②,過點![]() 的直線交
的直線交![]() 軸于點
軸于點![]() ,且
,且![]() 軸,點
軸,點![]() 是拋物線上
是拋物線上![]() ,
,![]() 之間的一個動點,直線
之間的一個動點,直線![]() ,
,![]() 與
與![]() 分別交于
分別交于![]() ,
,![]() ,當點
,當點![]() 運動時,
運動時,![]() 是否為定值?若是,試求出該定值;若不是,請說明理由.
是否為定值?若是,試求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“校同安全”受到全社會的廣泛關注,我市某中學對部分學生就校園安全知識的了解程度,采用隨機抽樣調查的方式,并根據收集到的信息進行統計,繪制了如圖兩幅尚不完整的統計圖,請你根據統計圖中所提供的信息解答下列問題:
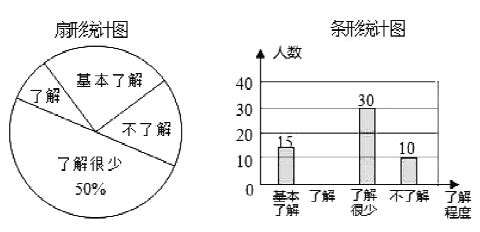
(1)接受問卷調查的學生共有 人,扇形統計圖中“了解”部分所對應扇形的圓心角為 度;并補全條形統計圖.
(2)若該中學共有學生![]() 人,請根據上述調查結果,估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數為 人;
人,請根據上述調查結果,估計該中學學生中對校園安全知識達到“了解”和“基本了解”程度的總人數為 人;
(3)若從對校園安全知識達到“了解”程度的![]() 個女生
個女生![]() 和
和![]() 個男生
個男生![]() 中分別隨機抽取
中分別隨機抽取![]() 人參加校園安全知識競賽,請用樹狀圖或列表法求出恰好抽到女生
人參加校園安全知識競賽,請用樹狀圖或列表法求出恰好抽到女生![]() 的概率.
的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對任意一個三位數n,如果n滿足各個數位上的數字互不相同,且都不為零,那么稱這個數為“相異數”,將一個“相異數”任意兩個數位上的數字對調后可以得到三個不同的新三位數,把這三個新三位數的和與111的商記為F(n).例如n=123,對調百位與十位上的數字得到213,對調百位與個位上的數字得到321,對調十位與個位上的數字得到132,這三個新三位數的和為213+321+132=666,666÷111=6,所以F(123)=6.
(1)計算:F(243),F(617);
(2)若s,t都是“相異數”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整數),規定:k=![]() ,當F(s)+F(t)=18時,求k的最大值.
,當F(s)+F(t)=18時,求k的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
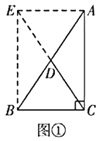
【題目】(教材呈現)下圖是華師版九年級上冊數學教材第103—104頁的部分內容.

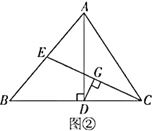
定理證明:請根據教材圖24.2.2的提示,結合圖①完成直角三角形的性質:“直角三角形斜邊上的中線等于斜邊的一半”的證明.
定理應用:如圖②,在![]() 中,
中,![]() ,垂足為點
,垂足為點![]() (點
(點![]() 在
在![]() 上),
上),![]() 是
是![]() 邊上的中線,
邊上的中線,![]() 垂直平分
垂直平分![]() .求證:
.求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
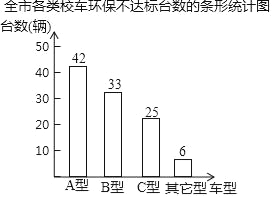
【題目】長春市對全市各類(A型、B型、C型.其它型)校車共848輛進行環保達標普查,普查結果繪制成如下條形統計圖:
(1)求全市各類環保不達標校車的總數;
(2)求全市848輛校車中環保不達標校車的百分比;
(3)規定環保不達標校車必須進行維修,費用為:A型500元/輛,B型1000元/輛,C型600元/輛,其它型300元/輛,求全市需要進行維修的環保不達標校車維修費的總和;
(4)若每輛校車乘坐40名學生,那么一次性維修全部不達標校車將會影響全市80000名學生乘校車上學的百分比是
查看答案和解析>>
科目:初中數學 來源: 題型:
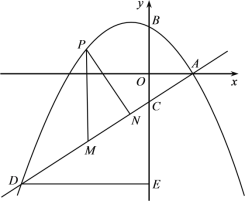
【題目】如圖,拋物線![]() 與
與![]() 軸交于點A(2,0),交
軸交于點A(2,0),交![]() 軸于點B(0,
軸于點B(0,![]() ),直線
),直線![]() 過點A與y軸交于點C,與拋物線的另一個交點為D,作DE⊥y軸于點E.設點P是直線AD上方的拋物線上一動點(不與點A、D重合),過點P作y軸的平行線,交直線AD于點M,作PN⊥AD于點N.
過點A與y軸交于點C,與拋物線的另一個交點為D,作DE⊥y軸于點E.設點P是直線AD上方的拋物線上一動點(不與點A、D重合),過點P作y軸的平行線,交直線AD于點M,作PN⊥AD于點N.
⑴填空:![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
⑵探究:是否存在這樣的點P,使四邊形PMEC是平行四邊形?若存在,請求出點P的坐標;若不存在,請說明理由;
⑶設△PMN的周長為![]() ,點P的橫坐標為x,求
,點P的橫坐標為x,求![]() 與x的函數關系式,并求出
與x的函數關系式,并求出![]() 的最大值.
的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com