
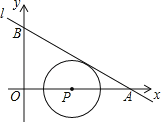
【題目】在直角坐標系中,我們將圓心坐標和半徑均為整數的圓稱為“整圓”.如圖所示,直線l:y=kx+4![]() 與x軸、y軸分別交于A、B,∠OAB=30°,點P在x軸上,⊙P與l相切,當P在線段OA上運動時,使得⊙P成為“整圓”的點P個數是_____個.
與x軸、y軸分別交于A、B,∠OAB=30°,點P在x軸上,⊙P與l相切,當P在線段OA上運動時,使得⊙P成為“整圓”的點P個數是_____個.
【答案】6.
【解析】
根據直線的解析式求得OB=4![]() ,進而求得OA=12,根據切線的性質求得PM⊥AB,根據∠OAB=30°,求得PM=
,進而求得OA=12,根據切線的性質求得PM⊥AB,根據∠OAB=30°,求得PM=![]() PA,然后根據“整圓”的定義,即可求得使得⊙P成為整圓的點P的坐標,從而求得點P個數.
PA,然后根據“整圓”的定義,即可求得使得⊙P成為整圓的點P的坐標,從而求得點P個數.
∵直線l:y=kx+4![]() 與x軸、y軸分別交于A、B,
與x軸、y軸分別交于A、B,
∴B(0,4![]() ),
),
∴OB=4![]() ,
,
在Rt△AOB中,∠OAB=30°,
∴OA=![]() OB=
OB=![]() ×4
×4![]() =12,
=12,
∵⊙P與l相切,設切點為M,連接PM,則PM⊥AB,
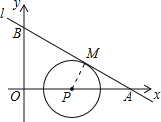
∴PM=![]() PA,
PA,
設P(x,0),
∴PA=12﹣x,
∴⊙P的半徑PM=![]() PA=6﹣
PA=6﹣![]() x,
x,
∵x為整數,PM為整數,
∴x可以取0,2,4,6,8,10,6個數,
∴使得⊙P成為整圓的點P個數是6.
故答案是:6.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
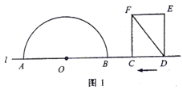
【題目】如圖1,點![]() 和矩形
和矩形![]() 的邊
的邊![]() 都在直線
都在直線![]() 上,以點
上,以點![]() 為圓心,以24為半徑作半圓,分別交直線
為圓心,以24為半徑作半圓,分別交直線![]() 于
于![]() 兩點.已知:
兩點.已知: ![]() ,
,![]() ,矩形自右向左在直線
,矩形自右向左在直線![]() 上平移,當點
上平移,當點![]() 到達點
到達點![]() 時,矩形停止運動.在平移過程中,設矩形對角線
時,矩形停止運動.在平移過程中,設矩形對角線![]() 與半圓
與半圓![]() 的交點為
的交點為![]() (點
(點![]() 為半圓上遠離點
為半圓上遠離點![]() 的交點).
的交點).
(1)如圖2,若![]() 與半圓
與半圓![]() 相切,求
相切,求![]() 的值;
的值;
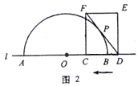
(2)如圖3,當![]() 與半圓
與半圓![]() 有兩個交點時,求線段
有兩個交點時,求線段![]() 的取值范圍;
的取值范圍;
(3)若線段![]() 的長為20,直接寫出此時
的長為20,直接寫出此時![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
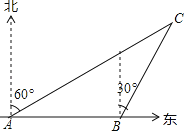
【題目】如圖,一艘漁船以60海里每小時的速度向正東方向航行.在A處測得燈塔C在北偏東60°方向上;繼續航行1小時到達B處,此時測得燈塔C在北偏東30°方向上.已知在燈塔C周圍50海里范圍內有暗礁,問這艘漁船繼續向東航行有無觸礁的危險?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題解決)
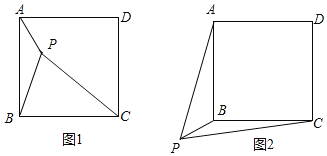
一節數學課上,老師提出了這樣一個問題:如圖1,點P是正方形ABCD內一點,PA=1,PB=2,PC=3.你能求出∠APB的度數嗎?
小明通過觀察、分析、思考,形成了如下思路:
思路一:將△BPC繞點B逆時針旋轉90°,得到△BP′A,連接PP′,求出∠APB的度數;
思路二:將△APB繞點B順時針旋轉90°,得到△CP'B,連接PP′,求出∠APB的度數.
請參考小明的思路,任選一種寫出完整的解答過程.
(類比探究)
如圖2,若點P是正方形ABCD外一點,PA=3,PB=1,PC=![]() ,求∠APB的度數.
,求∠APB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為半圓O的直徑,C為半圓上一點,AC<BC.
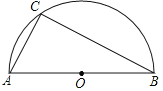
(1)請用直尺(不含刻度)與圓規在BC上作一點D,使得直線OD平分ABC的周長;(不要求寫作法,但要保留作圖痕跡)
(2)在(1)的條件下,若AB=10,OD=![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】英語老師對某班級全班同學進行口語測試,并按10分制評分,將評分結果制成了如圖兩幅統計圖(不完整).請根據圖表信息,解答下列問題:
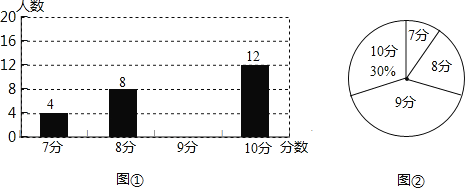
(1)求該班級學生總人數,并將條形統計圖補充完整;
(2)求該班學生口語測試所得分數的平均分;
(3)英語老師將隨機邀請該班一名同學進行口語對話,求事件“英語老師邀請得分為9分的同學進行口語對話”發生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
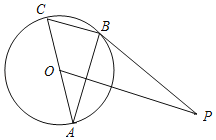
【題目】如圖,AC是⊙O的直徑,BC是⊙O的弦,點P是⊙O外一點,連接PB、AB,∠PBA=∠C.
(1)求證:PB是⊙O的切線;
(2)連接OP,若OP∥BC,且OP=4,⊙O的半徑為![]() ,求BC的長.
,求BC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“推進全科閱讀,培育時代新人”.某學校為了更好地開展學生讀書活動,隨機調查了九年級50名學生最近一周的讀書時間,統計數據如下表:
時間(小時) | 6 | 7 | 8 | 9 | 10 |
人數 | 5 | 8 | 12 | 15 | 10 |
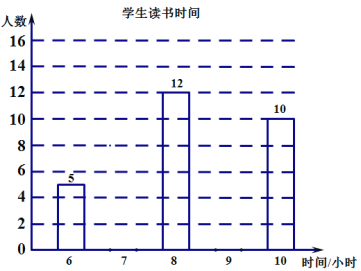
(1)根據上述表格補全下面的條形統計圖;
(2)寫出這50名學生讀書時間的眾數、中位數、平均數;
(3)若該校有1000名學生,求最近一周的讀書時間不少于7小時的人數?
查看答案和解析>>
科目:初中數學 來源: 題型:
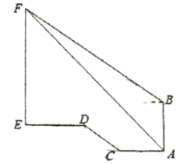
【題目】學校某數學興趣小組想測學校旗桿高度如圖,明明在稻香園一樓![]() 點測得旗桿頂點
點測得旗桿頂點![]() 仰角為
仰角為![]() ,在稻香園二樓
,在稻香園二樓![]() 點測得點
點測得點![]() 的仰角為
的仰角為![]() .明明從
.明明從![]() 點朝旗桿方向步行
點朝旗桿方向步行![]() 米到
米到![]() 點,沿坡度
點,沿坡度![]() 的臺階走到點
的臺階走到點![]() ,再向前走
,再向前走![]() 米到旗桿底部
米到旗桿底部![]() ,已知稻香園
,已知稻香園![]() 高度為
高度為![]() 米,則旗桿
米,則旗桿![]() 的高度約為( )(參考數據:
的高度約為( )(參考數據:![]() ,
,![]() ,
,![]() )
)
A.![]() 米B.
米B.![]() 米C.
米C.![]() 米D.
米D.![]() 米
米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com