
閱讀理解:對于任意正實數a、b,∵![]() ≥0, ∴
≥0, ∴![]() ≥0,
≥0,
∴![]() ≥
≥![]() ,只有當a=b時,等號成立.
,只有當a=b時,等號成立.
結論:在![]() ≥
≥![]() (a、b均為正實數)中,若ab為定值p,則a+b≥
(a、b均為正實數)中,若ab為定值p,則a+b≥![]() ,只有當a=b時,a+b有最小值
,只有當a=b時,a+b有最小值![]() .
.
根據上述內容,回答下列問題:
若m>0,只有當m= 時,![]() .
.
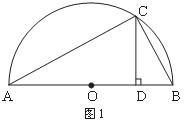
思考驗證:如圖1,AB為半圓O的直徑,C為半圓上任意一點(與點A、B不重合)過點C作CD⊥AB,垂足為D,AD=a,DB=b.
試根據圖形驗證![]() ≥
≥![]() ,并指出等號成立時的條件.
,并指出等號成立時的條件.
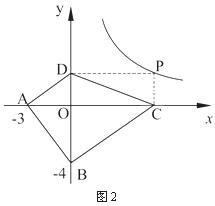
探索應用:如圖2,已知A(-3,0),B(0,-4),P為雙曲線![]() (x>0)上的任意一點,過點P作PC⊥x軸于點C,PD⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
(x>0)上的任意一點,過點P作PC⊥x軸于點C,PD⊥y軸于點D.求四邊形ABCD面積的最小值,并說明此時四邊形ABCD的形狀.
 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案科目:初中數學 來源: 題型:閱讀理解
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
 問欄桿多少長時,所用拉力F最小?是多少?
問欄桿多少長時,所用拉力F最小?是多少?查看答案和解析>>
科目:初中數學 來源: 題型:
| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
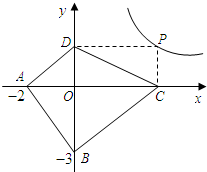 閱讀理解:對于任意正實數a,b,
閱讀理解:對于任意正實數a,b,| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 4 |
| x |
| 6 |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
| a |
| b |
| ab |
| ab |
| P |
| P |
| ab |

| 1 |
| m |
| 12 |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
 閱讀理解:
閱讀理解:| a |
| b |
| ab |
| ab |
| ab |
| p |
| p |
| 1 |
| m |
| 12 |
| x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com