【題目】某公司生產的某種產品每件成本為40元，經市場調查整理出如下信息：
①該產品90天售量(n件)與時間(第x天)滿足一次函數關系，部分數據如下表：
時間（第x天） | 1 | 2 | 3 | 10 | … |
日銷售量（n件） | 198 | 196 | 194 | ? | … |
②該產品90天內每天的銷售價格與時間（第x天）的關系如下表：
時間（第x天） | 1≤x＜50 | 50≤x≤90 |
銷售價格（元/件） | x+60 | 100 |
(1)求出第10天日銷售量；
(2)設銷售該產品每天利潤為y元，請寫出y關于x的函數表達式，并求出在90天內該產品的銷售利潤最大?最大利潤是多少?（提示：每天銷售利潤=日銷售量×（每件銷售價格－每件成本)）
(3)在該產品銷售的過程中，共有多少天銷售利潤不低于5400元，請直接寫出結果.
【答案】（1）180件；（2）第40天，利潤最大7200元；（3）46天
【解析】試題（1）根據待定系數法解出一次函數解析式，然后把x=10代入即可；
（2）設利潤為y元，則當1≤x＜50時，y=﹣2x2+160x+4000；當50≤x≤90時，y=﹣120x+12000，分別求出各段上的最大值，比較即可得到結論；
（3）直接寫出在該產品銷售的過程中，共有46天銷售利潤不低于5400元．
試題解析：解：（1）∵n與x成一次函數，∴設n=kx+b，將x=1，m=198，x=3，m=194代入，得： 
， 解得： 
，
所以n關于x的一次函數表達式為n=-2x+200；
當x=10時，n=-2×10+200=180．
（2）設銷售該產品每天利潤為y元，y關于x的函數表達式為： 
當1≤x＜50時，y=-2x2+160x+4000=-2（x-40）2+7200，
∵-2＜0，∴當x=40時，y有最大值，最大值是7200；
當50≤x≤90時，y=-120x+12000，
∵-120＜0，∴y隨x增大而減小，即當x=50時，y的值最大，最大值是6000；
綜上所述：當x=40時，y的值最大，最大值是7200，即在90天內該產品第40天的銷售利潤最大，最大利潤是7200元；
（3）在該產品銷售的過程中，共有46天銷售利潤不低于5400元．
奪冠訓練單元期末沖刺100分系列答案
新思維小冠軍100分作業本系列答案
名師指導一卷通系列答案科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．
（1）說明BE=CF的理由；
（2）如果AB=5，AC=3，求AE、BE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀材料：數學課上，吳老師在求代數式x2﹣4x+5的最小值時，利用公式a2±2ab+b2=（a±b）2，對式子作如下變形：x2﹣4x+5=x2﹣4x+4+1=（x﹣2）2+1，
因為（x﹣2）2≥0，
所以（x﹣2）2+1≥1，
當x=2時，（x﹣2）2+1=1，
因此（x﹣2）2+1有最小值1，即x2﹣4x+5的最小值為1．
通過閱讀，解下列問題：
（1）代數式x2+6x+12的最小值為 ；
（2）求代數式﹣x2+2x+9的最大或最小值；
（3）試比較代數式3x2﹣2x與2x2+3x﹣7的大小，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為推進垃圾分類，推動綠色發展，某工廠購進甲、乙兩種型號的機器人用來進行垃圾分類，甲型機器人比乙型機器人每小時多分20kg，甲型機器人分類800kg垃圾所用的時間與乙型機器人分類600kg垃圾所用的時間相等。
（1）兩種機器人每小時分別分類多少垃圾？
（2）現在兩種機器人共同分類700kg垃圾，工作2小時后甲型機器人因機器維修退出，求甲型機器人退出后乙型機器人還需工作多長時間才能完成？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖所示，工人師傅做一個矩形鋁合金窗框分下面三個步驟進行：
（1）先截出兩對符合規格的鋁合金窗料（如圖①所示），使
.
（2）擺放成如圖②的四邊形，則這時窗框的形狀是平行四邊形，它的依據是____________.
（3）將直尺緊靠窗框的一個角（如圖③），調整窗框的邊框，當直角尺的兩條直角邊與窗框無縫隙時（如圖④，說明窗框合格，這時窗框是矩形，它的依據是_____________________.
查看答案和解析>>
科目：初中數學 來源： 題型：
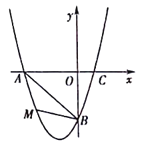
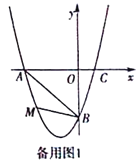
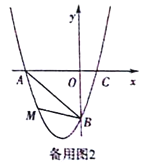
【題目】在平面直角坐標系中，已知拋物線經過A(－3，0)，B(0，－3)，C(1，0)三點.
(1)求拋物線的解析式；
(2)若點M為第三象限內拋物線上一動點，點M的橫坐標為m，△AMB的面積為S.求S
關于m的函數關系式，并求出S的最大值；
(3)若點P是拋物線上的動點，點Q是直線y=－x上的動點，判斷有幾個位置能夠使得點P、Q、B、O為頂點的四邊形為平行四邊形，直接寫出相應的點Q的坐標.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知如圖是三個方向看到的一個幾何體的形狀．
（1）寫出這個幾何體的名稱；
（2）寫出它的側面展開的形狀；
（3）若從正面看到的高為10cm，從上面看到的三角形的三邊長都為4cm，求這個幾何體的側面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】據我囯古代《周髀算經》記載，公元前1120年商高對周公說，將一根直尺折成一個直角，兩端連接得到一個直角三角形，如果勾是3，股是4，那么弦就等于5，后人概括為“勾三，股四、弦五”.像3、4、5這樣為三邊長能構成直角三角形的三個正整數，稱為勾股數.
（應用舉例）
觀察3，4，5； 5，12，13； 7，24，25；…
可以發現這些勾股數的勾都是奇數，且從3起就沒有間斷過，并且勾為3時，股
，弦
；勾為5時，股
，弦
；
請仿照上面兩組樣例，用發現的規律填空：
（1）如果勾為7，則股24=__________；弦25=___________.
（2）如果勾用
（
，且為奇數）表示時，請用含有的式子表示股和弦，則股=________；弦=_______.
（3）繼續觀察①4，3，5；②6，8，10；③8，15，17；…，可以發現各組的第一個數都是偶數，且從4起也沒有間斷過.請你直接用
（為偶數且
）的代數式來表示直角三角形的另一條直角邊和弦的長.
查看答案和解析>>
科目：初中數學 來源： 題型：
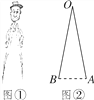
【題目】如圖①是一副創意卡通圓規，圖②是其平面示意圖，OA是支撐臂，OB是旋轉臂．使用時，以點A為支撐點，鉛筆芯端點B可繞點A旋轉作出圓．已知OA＝OB＝10cm.
(1)當∠AOB＝18°時，求所作圓的半徑(結果精確到0.01cm)；
(2)保持∠AOB＝18°不變，在旋轉臂OB末端的鉛筆芯折斷了一截的情況下，作出的圓與(1)中所作圓的大小相等，求鉛筆芯折斷部分的長度(結果精確到0.01cm，參考數據：sin9°≈0.1564，cos9°≈0.9877，sin18°≈0.3090，cos18°≈0.9511，可使用科學計算器)．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com